ein ausführlicher Rechenweg würde mir allerdings für mein Verständnis sehr gut tun.
Eine Verschiebung erfolgt über eine schlichte Addition um den Weg der Verschiebung. Eine Drehung erfolgt durch die Multiplikation einer komplexen Zahl mit dem Betrag \(=1\), deren Argument (der Winkel gegenüber der X-Achse) dem gewünschten Drehwinkel entspricht. Also genau in der Form, die lul schon angegeben hat: $$z_{-30°} = \cos 30° \colorbox{#ffff44}{-} i \sin 30°$$ (Minuszeichen da Rechtsdrehung, also mathematisch negativ). zur Veranschaulichung hilft eine Skizze der Szene:
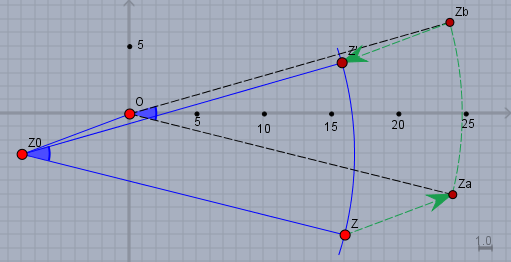
(Bem.: die Skizze zeigt eine Linksdrehung!)
Um den Punkt (bzw. die komplexe Zahl) \(z\) von \(z\) nach \(z'\) zu bringen (blauer Kreisbogen) fahren wir über den grün markierten Weg über \(z_a\) und \(z_b\) nach \(z'\). Die detaillierte Rechnung sieht dann so aus:
$$ \begin{aligned} z&=16-9i \\ z_0 &= -8-3i \\[4px] z_a &= z - z_0 = 16-9i - (-8-3i) \\ &= 24 - 6i\\[4px] z_b &= z_a \cdot (\cos 30° \colorbox{#ffff44}{-} i \sin 30°) \\&= (24 - 6i)(\frac12 \sqrt{3} \colorbox{#ffff44}{-} \frac12 i)\\ &= 12\sqrt{3} \colorbox{#ffff44}{-} 3 + ( \colorbox{#ffff44}{-}12 - 3\sqrt{3})i \\[4px] z' &= z_b + z_0 \\ &= 12\sqrt{3} \colorbox{#ffff44}{-} 3 + ( \colorbox{#ffff44}{-}12 - 3\sqrt{3})i -8-3i \\ &= 12 \sqrt{3} \colorbox{#ffff44}{-11} + ( \colorbox{#ffff44}{-15}-3\sqrt{3})i \\ &\approx \cancel{15,78 + 3,804 i} \space \colorbox{#ffff44}{9,78 - 20,20i} \end{aligned} $$
Ein Vorteil obiger Zeichnung ist, dass Du alle Zwischenergebnisse an der Zeichnung überprüfen kannst.