Hallo,
Wie genau kann ich mir eine Drehung um 45° gegen den Uhrzeigersinn vorstellen?
etwa so:
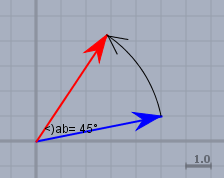
Der blaue Vektor \(a\) ist der Vektor $$a=\begin{pmatrix}5\\ 1\end{pmatrix}$$mittels Multiplikation mit einer Matrix wird daraus der rote Vektor \(b\):$$b = D_{45°} \cdot a = \frac12\sqrt2\begin{pmatrix}1& -1\\ 1& 1\end{pmatrix} \cdot \begin{pmatrix}5\\ 1\end{pmatrix} \approx \begin{pmatrix}2.828\\ 4.243\end{pmatrix}$$Die Drehmatrix ist also in diesem Fall$$D_{45°} = \begin{pmatrix}\cos(45°)& -\sin(45°)\\ \sin(45°)& \cos(45°)\end{pmatrix}=\frac12\sqrt2\begin{pmatrix}1& -1\\ 1& 1\end{pmatrix}$$
(i) Stellen Sie die Abbildung, die einen Vektor im \( \mathbb{R}^{2} \) um 45 Grad um den Ursprung gegen den Uhrzeigersinn dreht, als Matrix-Vektor-Multiplikation dar.
$$x \mapsto D \cdot x, \quad D= \frac12\sqrt2\begin{pmatrix}1& -1\\ 1& 1\end{pmatrix},\quad x \in \mathbb R^2$$
(ii) Bestimmen Sie die Determinante einer beliebigen Drehmatrix im \( \mathbb{R}^{2}( \) einer Matrix wie in (i)mit Winkel \( \alpha \in[0,2 \pi] \).
Berechne die Determinante: $$\det(D_{\alpha}) = \det \begin{pmatrix}\cos(\alpha)& -\sin(\alpha)\\ \sin(\alpha)& \cos(\alpha)\end{pmatrix} = \cos^2(\alpha) + \sin^2(\alpha) = 1$$
(iii) Welche der folgenden Matrizen beschreibt eine Drehung um den Ursprung im \( \mathbb{R}^{2} \) ? Begründen Sie.\( \left(\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right), \quad\left(\begin{array}{cc} 1 & 2 \\ -2 & 1 \end{array}\right) \)
die erste Matrix ist eine Drehmatrix. Ihre Determinante ist gleich 1 und es ist eine Orthogonalmatrix. Der Drehwinkel ist 90°.
Gruß Werner