die Länge eines Vektors berechnet sich aus der Wurzel der Summe aller Quadrate seiner Komponenten. Also ist z.B. der Vektor \(\vec{x}\) $$|\vec{x}| = \left| \begin{pmatrix} 3 \\ -5 \\2 \end{pmatrix}\right| = \sqrt{3^2 + (-5)^2 + 4^2} = \sqrt{50} = 5\sqrt{2}$$ \(5\sqrt{2} \approx 7,07\) Längeneinheiten lang. Um den Vektor \(\vec{x}\) auf eine Länge von 20 Längeneinheiten zu bringen muss man ihn also mit einem Faktor von \(20/ |\vec{x}|= 20 / (5\sqrt{2}) = 4/\sqrt{2} = 2\sqrt{2}\) multiplizieren. Da
$$2 \sqrt{2 } \cdot |\vec{x}| = 2 \sqrt{2} \cdot 5 \sqrt{2} = 20$$ ist. Somit ist $$Q = P + \frac{20}{|\vec{x}|} \vec{x} = \begin{pmatrix} 3 \\ 1 \\-5 \end{pmatrix} + 2\sqrt{2} \begin{pmatrix} 3 \\ -5 \\4 \end{pmatrix} = \begin{pmatrix} 3+6\sqrt{2} \\ 1-10\sqrt{2} \\ -5 + 8\sqrt{2} \end{pmatrix} \approx \begin{pmatrix} 11,49 \\ -13,14\\6,31 \end{pmatrix}$$
Ich habe Dir das ganze nochmal im Geoknecht3D eingegeben:
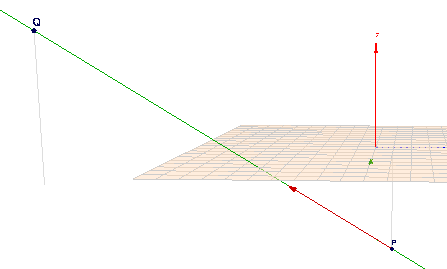
(klick auf das Bild und drehe die Szene mit der Maus)
Gruß Werner