Vektorrechnung Punktbestimmung

Question

Wie viele Punkte benötigt man im 3D- Raum um eine Gerade zu definieren ?

Wie lässt sich überprüfen, ob ein weiterer Punkt auf einer Geraden liegt ?

Answer 1

Wie viele Punkte benötigt man im 3D- Raum um eine Gerade zu definieren ?

Zwei.

Wie lässt sich überprüfen, ob ein weiterer Punkt auf einer Geraden liegt ?

Geradengleichung in Parameterform aufstellen, Punkt einsetzen. Der Punkt liegt genau dann auf der Geraden, wenn die entstandene Gleichung lösbar ist.

Comments

L = { } bedeutet schlichtweg es gibt keine Lösung, weil sich kein Element in der Lösungsmenge befindet.

Answer 2

Werner. Wie viele Punkte benötigt man im 3D-Raum um eine Gerade zu definieren?
Zwei.

Im Grunde nur \(\frac43\) Punkte ... ist aber schwierig das formal zu fassen.

Nachtrag:

ich habe mir was überlegt. Dazu ändere ich die Frage in:

Wie viele Punkte in 3D benötigt man, um drei (mehr oder weniger) beliebige und von einander (weitgehend) unabhängige Geraden zu definieren?

Die Antwort ist: vier!

Dafür habe ich mir eine Definition ausgedacht, die zwar nicht perfekt ist, aber für drei vogelwild liegende Geraden passt. Ich bin mir dessen bewusst, dass ich damit nicht jede Gerade bzw. Geradenkombination darstellen kann. Die Geraden dürfen nicht parallel verlaufen und es dürfen auch keine zwei der drei Geraden parallel zur XY-Ebene verlaufen, u.a.. Aber ich behaupte mal frech und ohne Beweis, dass der Quotient der Anzahl der darstellbaren Geradentripel geteilt durch die Anzahl aller möglichen Tripel in 3D gleich 1 ist!

Zunächst definiere ich eine Basisebene - das sei die XY-Ebene. Dann wähle ich bei jeder der Geraden genau den Punkt auf der Geraden, dessen Projektion auf die Basisebene am dichtesten am Ursprung liegt. Diesen Punkt nenne ich den Referenzpunkt \(R\) der Geraden. Der Vektor vom Ursprung zur Projektion des Referenzpunktes auf die Basisebene sei der Normalenvektor einer weiteren Ebene, die ich Referenzebene der Geraden nenne. Alle Referenzebenen stehen notwendigerweise senkrecht auf der Basisebene und enthalten 'ihre' Gerade. Jetzt bildet man von den drei Geraden jeweils noch eine Ebene, die senkrecht auf der jeweiligen Referenzebene steht und ebenfalls ihre Gerade beinhaltet. Das mache ich für drei Geraden, somit bleibt noch ein Punkt über. Der vierte Punkt ist nun der Schnittpunkt der drei Ebenen, die senkrecht auf den Referenzebenen stehen. Diesen Punkt nenne ich den gemeinsamen Projektionspunkt \(P\).

Umgekehrt kommt man zu einer Geraden durch ihren Referenzpunkt und den gemeinsamen Projektionspunkt, dessen Projektion \(P'\) auf die Referenzebene einen zweiten Punkt der Geraden definiert. Ein Bild dazu:

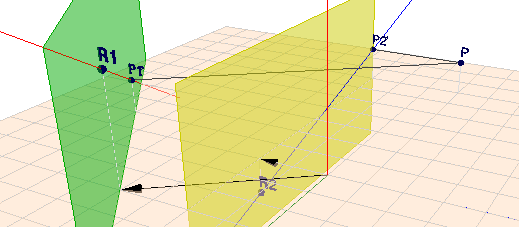
oben habe ich zwei der drei Geraden eingezeichnet (rot und blau). Mit ihren Referenzpunkten \(R_1\) und \(R_2\) sowie der Referenzebene \(E_1\) (grün)  und \(E_2\) (gelb).

Ja - und wenn man für drei Geraden vier Punkte benötigt, so braucht man pro Gerade \(\frac43 \) Punkte.

Du brauchst es auch nicht selber erklären, wenn du einen Link kennst ...

:-) Der Link geht an den Bio-Server zwischen meinen Ohren. Frei nach dem Motto: Denken ist wie googeln nur krasser.

Gruß Werner

Comments

Hallo Werner.

Könntest du das etwas näher erläutern. Kann auch im 2-Dimensionalen sein. Braucht man dort auch 4/3 Punkte oder sogar noch weniger?

Du brauchst es auch nicht selber erklären, wenn du einen Link kennst oder ein Buch empfehlen kannst.

---

Kann auch im 2-Dimensionalen sein. Braucht man dort auch 4/3 Punkte oder sogar noch weniger?

Ein Punkt in 3D beinhaltet 3 Informationen (die drei Koordinaten). Zwei Punkte in 3D sind bereits 6 Informationen. Wird eine Gerade in 3D mit zwei Punkten beschrieben, so ist sie bereits überbestimmt, da mit den zwei Punkten auch die (eindimensionale) Position der Punkte auf der Geraden selbst mit angegeben ist - also zweimal eine Information zu viel.

Für eine Gerade in 2D braucht man nur zwei Informationen. Z.B. \(m\) und \(b\) in \(y=mx+b\).

Für eine Gerade in 3D könnte man eine Spurgerade z.B. in der XY-Ebene  (mit zwei Informationen) beschreiben. Damit wäre die Ebene, die die Spurgerade enthält und senkrecht auf der XY-Ebene steht, eindeutig beschreiben. Und innerhalb dieser Ebene könnte man mit zwei weiteren Informationen eine Gerade beschreiben. Die Gerade wäre so eindeutig mit 4 Informationen in 3D beschrieben.

BTW.: Wir können uns sicher auch darauf einigen, dass \(\lceil \frac43 \rceil = 2\) ist, wenn nur ganze Punkte erlaubt sind ;-)

---

Ich hätte es lustiger gefunden, wenn wir über \(\frac43\) Punkte diskutieren und nicht über die Mehrdeutigkeiten von Sprache.

Schade!

---

Ich habe gerade die beiden Stränge geteilt, so gut es ging.

Dieser Ansatz würde mich auch genauer interessieren.

---

Für eine Gerade in 2D braucht man nur zwei Informationen. Z.B. m und b in y=mx+b.

Damit können Geraden parallel zur y-Achse nicht beschrieben werden. Und für die allgemeinere Form ay + bx = c benötigt man wiederum drei Informationen.

---

@Oswald:

Es steht Z.B. m und b.

ay + bx = c

kannst du normieren auf rx + sy=1.

---

ay + bx = c  kann man nur dann auf rx + sy=1 normieren, wenn c ≠ 0 ist, wenn die Gerade also nicht durch den Ursprung verläuft.

---

@Oswald. Richtig!

---

In der Ebene kannst du schlicht 2 Punkte einzeichnen. Diese mit A und B beschriften und die Gerade ist festgelegt.

Ein Koordinatensystem braucht es dazu nicht.

BTW.: Wir können uns sicher auch darauf einigen, dass ⌈4/3⌉=2
ist, wenn nur ganze Punkte erlaubt sind ;-)

:D

---

oben in der Antwort eine mögliche Definition angefügt, wie man mit \(\frac43\) Punkte pro Gerade hinkommt.

Gruß Werner

Answer 3

wenn die entstandene Gleichung lösbar ist.

sollte wohl besser

"wenn die entstandene Gleichung erfüllbar ist."

oder

"wenn die entstandene Gleichung eine Lösung hat ."

lauten.

Comments

@-Wolfgang- Das sind nach meinem Sprachgebrauch Synonyme. Zeige mir ein Beispiel, in dem diese Aussagen unterschiedliche Bedeutung haben.

@Werner-Salomon Versuch trotzdem mal, das formal zu fassen; ich bin gespannt. Für mich ist eine Gerade ein eindimensionaler affiner Unterraum.

---

@Oswald

Wenn du für eine Gleichung ggf. L = { } bestimmt hast, hast du sie gelöst.

Sie ist dann also "lösbar", aber nicht "erfüllbar".

Dein "Sprachgebrauch" wird leider oft benutzt . Nach meiner Meinung ist er aber nicht korrekt.

---

Erfüllbar ist doch eine Gleichung, wenn sie mind. eine Lösung hat oder liege ich da jetzt falsch?

---

Genau so sehe ich das auch.

Lösbar ist sie aber, wenn man die Lösungsmenge bestimmen kann, auch wenn diese leer ist.

---

@Wolfgang: lösbar kommt vier mal vor im Wikipediatext über Gleichung: Bsp. https://de.wikipedia.org/wiki/Gleichung#Bestimmungsgleichungen

---

Wolfgang ist superschlau. Er kann jede Gleichung lösen, auch die, die bisher als unlösbar gelten. Ganz einfach. Die Lösungsmenge ist dann einfach leer ;-)

---

@Lu

Das ist mir durchaus bekannt:

Dein "Sprachgebrauch" wird leider oft benutzt . Nach meiner Meinung ist er aber nicht korrekt.

Erfüllbar ist doch eine Gleichung, wenn sie mind. eine Lösung hat oder liege ich da jetzt falsch?

Genau so sehe ich das auch.
Wenn du für eine Gleichung ggf. L = { } bestimmt hast, hast du sie gelöst.
Sie ist dann also "lösbar", aber nicht "erfüllbar".

---

@Mathecoach

Wolfgang ist superschlau. Er kann jede Gleichung lösen, auch die, die bisher als unlösbar gelten.

Das geht wohl an der ganzen Diskussion völlig vorbei. Oder kannst du das näher begründen?

---

Ich sehe das wie Lu: eine Gleichung deren Lösungsmenge leer ist, ist unlösbar.

Und so findest du es auch bei Wikipedia.

Was hätte es ansonsten für einen Sinn wenn man nach lösbar und unlösbar unterscheidet.

Wenn eine Gleichung also eine Lösung hat, die du nur numerisch angeben kannst, deren Lösungsmenge du also nicht exakt angeben kannst, ist sie dann lösbar oder unlösbar.

---

@Lu

In deiner Grundmenge ℝ gilt  x² ≥ 0.

-2 < 0   →  L = { }

Damit ist die Gleichung gelöst, also lösbar.

Sie ist aber nicht erfüllbar.

Es handelt sich hier nicht um ein mathematisches, sondern um ein sprachliches Problem!

---

Wenn du für eine Gleichung ggf. L = { } bestimmt hast, hast du sie gelöst. Sie ist dann also "lösbar", aber nicht "erfüllbar".

Heist das, dass du eine Gleichung als lösbar bezeichnen würdest, sobald sie eine Lösungsmenge hat? Dann ist jede Gleichung lösbar und es gibt keinen Grund, das Wort überhaupt zu verwenden.

---

Ich finde die andere Diskussion auch spannender. Sie hat jetzt einen eigenen Strang.

Den Sprachgebrauch in Wikipedia würde ich hinnehmen. Da hat es keinen Sinn dagegen anzureden und noch weniger eigene Begrifflichkeiten wie "Gleichung erfüllen" zu prägen. "Bedingungen" kann man erfüllen. 

---

@Oswald

Dann ist jede Gleichung lösbar und es gibt keinen Grund, das Wort überhaupt zu verwenden.

Du hast es verwendet, nicht ich!

---

@Mathecoach

Dann ist jede Gleichung lösbar und es gibt keinen Grund, das Wort überhaupt zu verwenden.

Ich verwende beide Begriffe bei Gleichungen genau aus diesem Grund nur dann, wenn sie mir - wie hier - aufgezwungen werden :-)

Wegen des allgemein üblichen Sprachgebrauchs (eigentlich Sprachmissbrauchs) steht in meinem ersten Kommentar auch nichts von "falsch" sondern

... sollte wohl besser ...

Nachtrag: 
Wer Letzterem nicht zustimmen kann, liegt halt außerhalb meines Sprachgefühls :-)

---

Für eine Gerade in 2D braucht man nur zwei Informationen. Z.B. m und b in y = mx + b.

Der y-Achsenabschnitt b ist doch der Punkt (0 | b) und damit sind dies auch 2 Informationen. Die Steigung bedeutet doch wenn man eine Einheit in x-Richtung geht muss man m Einheiten in y-Richtung gehen um auf der Geraden zu bleiben. Die Steigung m kann man also als Richtungsvektor (1, m)^T ansehen. Dann hätten wir schon 4 Informationen.

Man kann die Gerade also in der Parameterform

X = [0, b] + r * [1, m]

schreiben.

Langen für eine Gerade im 2-D also wirklich 2 Informationen oder müsste es zwei Bedingungen lauten.

Für die allgemeine lineare Funktion y = m*x + b braucht man 2 Bedingungen um m und b eindeutig bestimmen zu können.

Nun merkt man das die lineare Funktion y = m*x + b aber gar nicht alle 2-D Geraden beschreiben kann. Unendlich viele Geraden lassen sich damit gar nicht beschreiben.

Also langen für die Beschreibung einer Geraden im 2-D keine 2 Informationen.

2 Bedingungen wie 2 Punkte langen. Das sind aber schon 4 Informationen.

---

@Lu

wieso ist dein Kommentar, der meinem Kommentar

@Lu

In deiner Grundmenge ℝ gilt  x² ≥ 0.

-2 < 0  →  L = { }

Damit ist die Gleichung gelöst, also lösbar.

Sie ist aber nicht erfüllbar.

Es handelt sich hier nicht um ein mathematisches, sondern um ein sprachliches Problem!

vorherging, plötzlich (kommentarlos) verschwunden 

und meiner dadurch völlig ohne Zusammenhang?

---

Ich habe gerade die beiden Stränge geteilt, so gut es ging.

Dem ist nicht so!

Mein letztes Wort:

eigene Begrifflichkeiten wie "Gleichung erfüllen" zu prägen. "Bedingungen" kann man erfüllen.

Der Begriff "Gleichung erfüllbar" wurde nicht von mir "geprägt", sondern - z.B. in Lehrpänen - von anderen, die ein gesundes Sprachgefühl haben.

Wer dem " ... sollte wohl besser ... " in meinem Ausgangskommentar nicht zustimmen kann, liegt halt außerhalb dieses Sprachgefühls.

Jeder Versuch, dieses " ... sollte wohl besser ... "  logisch zu widerlegen, ist in meinen Augen absurd!

Und jeder, der Wikipedia für der Weisheit letzten Schluss hält, sollte sich hier den zweiten Satz "reinziehen":

https://de.wikipedia.org/wiki/Erf%C3%BCllbarkeit

Und: Formulierungen wie

Wolfgang ist superschlau.

und andere überflüssige Spitzen sollte der betreffende Redakteur sich endlich mal abschminken (auch wenn er sie selbst vielleicht nicht als solche empfindet), womit wir mal wieder beim Sprachgefühl wären.

---

Da hättest du auch gleich das Beispiel anführen können

Beispiele: In der Theorie der reellen Zahlen (also dem üblichen Zahlensystem) ist die Gleichung 2x + 1 = 3x lösbar, also diese Aussage erfüllbar.

Das Gleichungssystem x < 0, x^{2} ≤ 0 ist dagegen nicht lösbar, denn die einzige Lösung für x^{2} ≤ 0 wäre x = 0, aber diese Lösung erfüllt nicht x < 0. Diese Aussage ist also nicht erfüllbar.

https://de.wikipedia.org/wiki/Erfüllbarkeit

nicht lösbar ist auch unlösbar oder nicht ?

---

Habe nie bestritten, dass Wikipedia die Begriffe synonym verwendet.

Es ging mir hier um "gesundes" Sprachempfinden!

und diese Sätze lassen dieses vermissen. 

---

Du solltest nicht mit Empfinden und Meinungen argumentieren. Das hat in der Mathematik nichts zu suchen.

Wir wissen doch beide das x = 0 und x = 5 keine mathematische Lösung sein kann auch wenn wir das so Meinen oder Empfinden.

---

Du solltest nicht mit Empfinden und Meinungen argumentieren. Das hat in der Mathematik nichts zu suchen.

Es gibt keinen Freibrief für Sprachmissbrauch für die Mathematik, und diesen werde ich kritisieren, wo immer ich ihn finde! Das hat damit überhaupt nichts zu tun. 

Wenn etwas seltsam ist, wird "Das ist komisch" nicht dadurch richtig, dass "komisch" häufig an Stelle von "seltsam"  verwendet (missbraucht!) wird.

Weitere Kommentare sollten sich endlich an meinem Ausgangskommentar - denn um diesen ging es! - orientieren.

Und alles was da steht, ist schlicht und einfach richtig!!

---

Und nur weil du meinst

x^2 = -1

ist lösbar im Bereich der reellen Zahlen weil sich ja als Lösungsmenge die leere Menge angeben lässt, dann ist das hochgradiger Unsinn in meinen Augen. Und das werde ich immer kritisieren.

Und das hat nun wirklich überhaupt nichts mit Sprachmissbrauch zu tun.

---

Mit Blick auf den allgemeinen Sprachgebrauch habe ich das in meinem Ausgangskommentar auch nicht getan.

was verstehst du an

... sollte wohl besser ...

nicht?

Die zitierte Formulierung diente später lediglich der sprachlichen Verdeutlichung.

(Deshalb wirst du es bei mir auch nie wieder kritisieren können :-))

Und wenn jemand die gelöste Gleichung

x² = -1      in der Grundmenge ℝ  

mit der Lösungsmenge  L = { }

als "nicht lösbar"  bezeichnet,

ist das für mich Vergewaltigung der deutschen Sprache!

Und das hat sehr viel mit Sprachgebrauch zu tun!

---

A: "Aufgabe: Finde eine reelle Zahl, für die gilt x^2=-1"

B:"Eine solche Zahl gibt es nicht. Die Aufgabe ist nicht lösbar."

---

@Gast jc2144: Keine Antwort auf die Frage. Für den Fragesteller allenfalls amüsanter Disput. Daher separiert.

---

L = { } ist die formelle Angabe aller Lösungen. Wenn eine leere Lösungsmenge angegeben wird bedeutet es, es gibt keine Lösung. Und wenn es keine Lösung gibt dann ist die Aufgabe eben nicht lösbar.

---

Ich verweise auf die (jetzt!) Antwort!
Dort steht nichts von "falsch"
Was versteht ihr nicht an

... sollte wohl besser ...

@jc144

Eine solche Zahl gibt es nicht. Die Aufgabe ist nicht lösbar."

Das ist die Lösung der Aufgabe.

Die Aufgabe ist keine Gleichung!

@Mathecoach

... die Aufgabe eben nicht lösbar.

Mit der Bestimmung von L ist die Aufgabe gelöst.
Das Problem liegt einfach nur darin, dass der Begriff "Lösung" sowohl für die Elemente, die die Gleichung erfüllen als auch für den Vorgang des Lösens einer Aufgabe - also für zwei völlig verschiedene Dinge benutzt wird. Und schon das allein macht den allgemein üblichen Umgang mit den Begriffen sprachlich grenzwertig. 

Für mehrere Menschen - also euch - ist es natürlich sehr einfach, einen Einzelnen so lange (ohne auf dessen eigentliche Antwort überhaupt einzugehen) zu nerven, bis er keine Lust mehr hat. 
Und genau das ist genau jetzt bei mir endgültig eingetreten :-)