Kettenregel. Wann ändert sich in Stockholm die Tageslänge am schnellsten?

Question

Im Verlauf eines Jahres ändert sich die Tageslänge. Für die Stadt Stockholm kann sie modellhaft beschrieben werden durch eine Funktion f mit f(x)=12+6,24sin(pi/6*x). Dabei ist x die Zeit in Monaten ab 21. März und f(x) die Tageslänge in Stunden. Wann ändert sich in Stockholm die Tageslänge am schnellsten? Wie groß ist die Tageslänge dann?

Bitte eine Antwort mit Erklärung bzw. Rechenweg.

Danke

Answer 1

Wann ändert sich in Stockholm die Tageslänge am schnellsten?

Das ist entweder am 21. März oder an einer der Wendestellen der Funktion f.

Berechne zu allen vier Zeitpunkten die Ableitung und nimm den Zeitpunkt, zu dem diese den größten Betrag hat.

Comments

Ich habe versucht die Wendestellen zu berechnen durch die zweite Ableitung =0 aber ich hab es nicht bis zur Ende geschafft.

Bin bei

-6,24sin(pi/6*x)*(pi/6)^2=0 angekommen

Weiter weiß ich nicht

---

Bin bei -6,24sin(pi/6*x)*(pi/6)²=0 angekommen

Dividiere durch -6,24 und dann durch (π/6)².

Deine zweite Ableitung ist richtig.

---

Und das ist sin(pi/6*x)=0

Und wie gehts jetzt weiter?

---

Die Umkehrfunktion der Sinusfunktion anwenden. Die heißt üblicheweise arcsin, wird aber auch manchmal (insb auf Taschenrechnern) mit sin^-1 bezeichnet:

sin(π/6 · x) = 0    | arcsin

π/6 · x = arcsin(0) + 2πn oder π/6 · x = π - arcsin(0) + 2πn   | · 6/π

x = 6/π · arcsin(0) + 6/π · 2πn oder x = 6/π · π - 6/π · arcsin(0) + 6/π · 2πn

Dabei kann n jede ganze Zahl sein. Der Summand 2πn kommt wegen der Periodizität der Sinusfunktion zuastande.

Answer 2

f(x)=12+6,24sin(pi/6*x). Dabei ist x die Zeit in Monaten ab 21. März und f(x) die Tageslänge in Stunden. Wann ändert sich in Stockholm die Tageslänge am schnellsten? Wie groß ist die Tageslänge dann?

Dies ist die Frage nach der Wendestelle
Funktion
1.Ableitung
2.Ableitung

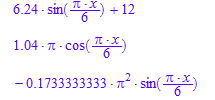
2.Ableitung = 0
Satz vom Nullprodukt anwenden

sin (x * π / 6 ) = 0
Die sin-Funktion ist bei 0,π,2π usw = 0

sin (x * π / 6 ) = sin( 0 )
x * π / 6 = 0
x = 0  => 21.3.

sin (x * π / 6 ) = sin( π )
x * π / 6  = π
x = 6 => 21.9.

Bei Bedarf weiterfragen.