nicht verzweifeln. So ein Unterraum in \(\mathbb{R}^3\) mit zwei Basisvektoren ist doch nichts anderes als eine Ebene. Da sind also zwei Ebenen und ihr Schnitt sollte i.A. eine Gerade betragen, falls sie nicht gerade parallel liegen. Man kommt zur Geraden, indem man die Ebenen einfach gleich setzt. Alle Punkte, die auf beiden Ebenen liegen, gehören zur Schnittgeraden.
$$v_1 \cdot r + v_1 \cdot s = u_1 \cdot t + u_2 \cdot u$$ das bringe ich auf eine Seite ... $$v_1 \cdot r + v_1 \cdot s - u_1 \cdot t - u_2 \cdot u = 0$$ ...und gleich in Matrizenform: $$\left( \begin{array}{cccc|c} 1 & 0& -2 & -1 & 0\\ 3 & 1 & -1 &-1 & 0\\ 2 & 1 & -0 & -1 & 0\end{array} \right)$$ und dies formt man nun durch Äquivalenzumformungen (Gauß-Algorithmus) um; zu: $$\left( \begin{array}{cccc|c}1 & 0 & 0 & 1 & 0\\ 0 & 1 & 0 & -3 & 0 \\ 0 & 0 & 1 & 1 & 0\end{array} \right)$$ Ich setze nun \(u=\lambda\), dann ist \(t=-\lambda\) und dies setze ich in die zweite Basis ein: $$V \cap U: \vec{x} = \begin{pmatrix} 2\\1 \\ 0\end{pmatrix} (- \lambda) + \begin{pmatrix} 1\\1 \\ 1\end{pmatrix} \lambda = \begin{pmatrix} -1\\0 \\ 1\end{pmatrix} \lambda$$ Eine Basis für den Schnitt \(V \cap U\) ist also $$w = \begin{pmatrix} -1\\0 \\ 1\end{pmatrix}$$
Und anbei nochmal zur Anschauung in Geoknecht3D
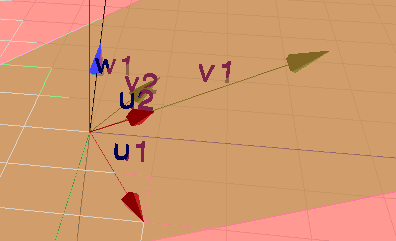
(klick auf das Bild)
Gruß Werner