Parabelgleichung für Rinne mit Tiefe h und Breite 2a bestimmen?

Question

Hallo

Aufgabe:

Eine Rinne der Tiefe h und der Breite 2a habe einen Querschnitt in der Gestalt einer Parabel. Wie groß muss die Tiefe H einer Rinne mit rechteckigem Querschnitt sein, damit die Querschnitte beider Rinnen gleich groß sind ? Fertigen Sie zunächst eine Skizze an und stellen Sie die Parabelgleichung auf.

Ich bin wie folgt vorgegangen:

$$A(Parabel)=2a*h-\int_{-a}^{a}f(x)$$

$$A(eckig)=2a*H$$

$$2a*h-\int_{-a}^{a}f(x)=2a*H$$

$$H=h-\frac{\int_{-a}^{a}f(x)}{2a}$$

Und wie stelle ich da nun eine Parabelgleichung auf ? Kann das nicht eine x-beliebige sein?

Comments

Eine Parabelgleichung für die Rinne gibt es bereits hier: https://www.mathelounge.de/369825/rinne-mit-querschnitt-parabel-flacheninhalt-rechteck

Answer 1

Ich würde so vorgehen:

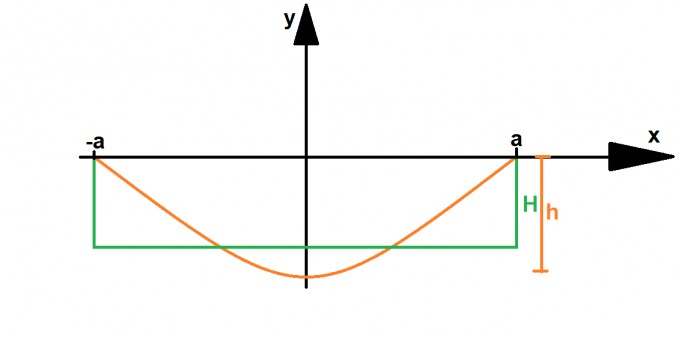
Die orange Kurve ist die parabelförmige und das grüne die rechteckige Regenrinne.

Die Parabel hätte aus der Skizze demnach diese Gestalt:

$$ f(x)=k\cdot x^2+b $$

Sie soll folgende Bedingungen erfüllen

$$ f(0)=-h\\f(a)=f(-a)=0 $$

Das ergibt dann folgende Parabelgleichung:

$$ f(x)=\frac{h}{a^2}\cdot x^2-h=h\cdot \Big(\frac{1}{a^2}\cdot x^2-1 \Big) $$

Nun die Querschnittsfläche davon:

$$ \int_{-a}^a \Bigg(h \cdot \Big(\frac{1}{a^2}\cdot x^2-1 \Big)\Bigg) dx=2\cdot h \int_{0}^a \Big(\frac{1}{a^2}\cdot x^2-1 \Big) dx\\=2\cdot h\cdot \Big[\frac{1}{3\cdot a^2}\cdot x^3-x \Big]_0^a=\frac{2}{3}\cdot a\cdot h-a\stackrel{!}{=}2\cdot a\cdot H\\ \Leftrightarrow H=\frac{1}{3}\cdot h-\frac{1}{2}  $$

Answer 2

Hallo

du hast das wichtigste vergessen:"Fertigen Sie zunächst eine Skizze an!

 das ist eine Parabel die in der Höhe h die Breite 2a hat.

also am besten symmetrisch zur y-Achse und dann bei y=h x=a

Ansatz y=c*x^2, daraus h=c*a^2 c=h/a^2

deine Parabel ist also f(x)=h/a^2*x^2,

Gruß lul