Die Frage ist doch: was hat die Aufgabe mit 'Ähnlichkeit' zu tun? Dazu muss man in diesem Fall etwas über den Horizont bzw. über das Quadrat hinaus denken:
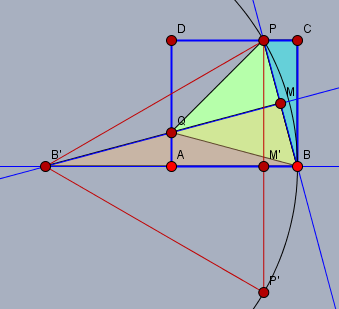
man kann sich überlegen, dass das Dreieck \(\triangle B'BM\) ähnlich dem Dreieck \(\triangle BCP\) ist. Weiter ist \(|B'B|=|B'P|\) Dann kann man sich überlegen, dass das Dreieck \(\triangle B'P'P\) ebenso ein gleichseitiges ist, mit der Kantenlänge \(2a\) ist. Dann muss \(|AM'|=|DP| = (\sqrt{3}-1)a\) sein und aus dem Dreieck \(\triangle QPD\) folgt dann nach Pythagoras die Kantenlänge \(s\) des gesuchten gleichseitigen Dreiecks:
$$s = (\sqrt{3}-1)a \cdot \sqrt{2}= a(\sqrt{6}-\sqrt{2})$$
was übrigens identisch mit \(s=4a/(\sqrt{6} + \sqrt{2})\) ist.