du kannst dir das an so einem Bild verdeutlichen:
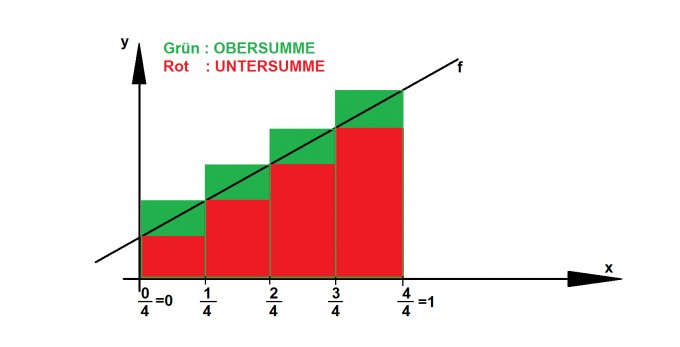
Du hast n hier n=4) Teilflächen.
Die k-te Fläche (ein Rechteck) berechnet sich durch $$ A_k=b\cdot l= \frac{1}{4}\cdot f\Big(\frac{k}{4}\Big)$$
Die Breite b ist hier 1/4, da du das Intervall [0,1] in vier Teile geteilt hast.
Für die jeweilige Summe ist es nun wichtig, wo angefangen wird aufzusummieren. Bei der Obersumme geht es bei x=1/4 los und endet bei x=1, bei der Untersumme geht man um eine Einheit nach links, sodass man bei x=0 anfängt und bei x=3/4 endet.
OBERSUMME
$$ O_4=A_1+A_2+A_3+A_4\\=\frac{1}{4}\cdot f\Big(\frac{1}{4}\Big)+\frac{1}{4}\cdot f\Big(\frac{2}{4}\Big)+\frac{1}{4}\cdot f\Big(\frac{3}{4}\Big)+\frac{1}{4}\cdot f\Big(\frac{4}{4}\Big)\\=\frac{1}{4}\cdot\Bigg( f\Big(\frac{1}{4}\Big)+f\Big(\frac{2}{4}\Big)+ f\Big(\frac{3}{4}\Big)+f\Big(\frac{4}{4}\Big)\Bigg)\\=\frac{1}{4}\cdot\Bigg(\Big(\frac{1}{4}+1\Big)+\Big(\frac{2}{4}+1\Big)+\Big(\frac{3}{4}+1\Big)+\Big(\frac{4}{4}+1\Big)\Bigg)\\=\frac{1}{4^2}\cdot (5+6+7+8)=\frac{26}{16}=1,625 $$
UNTERSUMME
$$ U_4=A_0+A_1+A_2+A_3\\=\frac{1}{4}\cdot f\Big(\frac{0}{4}\Big)+\frac{1}{4}\cdot f\Big(\frac{1}{4}\Big)+\frac{1}{4}\cdot f\Big(\frac{2}{4}\Big)+\frac{1}{4}\cdot f\Big(\frac{3}{4}\Big)\\=\frac{1}{4}\cdot\Bigg( f\Big(\frac{0}{4}\Big)+f\Big(\frac{1}{4}\Big)+ f\Big(\frac{2}{4}\Big)+f\Big(\frac{3}{4}\Big)\Bigg)\\=\frac{1}{4}\cdot\Bigg(\Big(\frac{0}{4}+1\Big)+\Big(\frac{1}{4}+1\Big)+\Big(\frac{2}{4}+1\Big)+\Big(\frac{3}{4}+1\Big)\Bigg)\\=\frac{1}{4^2}\cdot (4+5+6+7)=\frac{22}{16}=1,375 $$
Also ist $$ U_4=1,375\leq A \leq 1,625=O_4 $$
Genauso gehst du bei den anderen vor.