Ganzrationale Funktion dritten Grades gesucht

Question

Ich habe zur Zeit Probleme mit folgender Aufgabe:

Gesucht ist eine ganzrationale Funktion dritten Grades f(x), deren Graph in P(0/0) die Steigung m = 9/4 hat und in Z(9/0) die x-Achse berührt.

Answer 1

der Ansatz ist $$ f(x)=ax^3+bx^2+cx+d\\f'(x)=3ax^2+2bx+c$$

Nun die Eigenschaften

P(0/0)

f(0)=0 => d=0

In P die Steigung m=9/4

f'(0)=9/4 => c=9/4

Punkt Z(9/0)

f(9)=0=729a+81b+9/4

Z ist ein Berührpunkt, also

f'(9)=0=243a+18b+9/4

Ein 2x2 LGS ist dann nur noch zu lösen, um a und b zu kennen. Fertig.

Answer 2

Hallo Gymi,

$$f(x) = ax^3+bx^2+cx+d\\f'(x)=3ax^2+2bx+c$$

P(0|0), Steigung = 9/4

f(0) = 0 ⇒ d = 0

f'(0) = 9/4 ⇒ c = 9/4

Punkt Z(9|0) berührt die x-Achse, also liegt hier eine Extremstelle vor (f'(x) = 0)

f(9) = 0 ⇒ 729a + 81b + 81/4 = 0

f'(9) = 0 ⇒ 243a + 18b + 9/4 = 0

Lösung dieses Gleichungssystems ergibt für a = 1/36 und b =  -1/2

Bei Fragen bitte melden!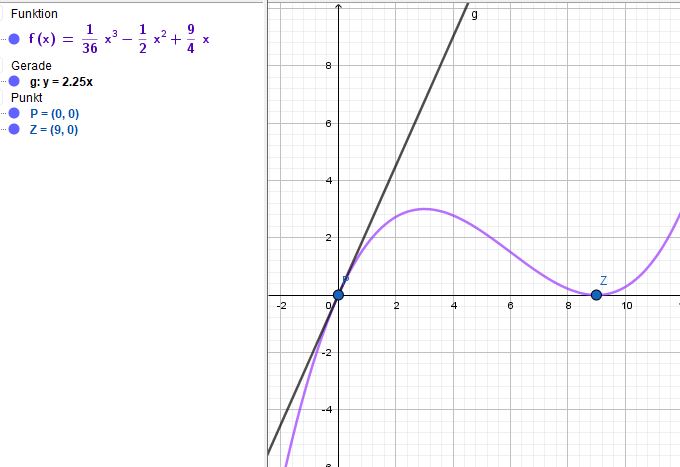

Gruß, Silvia

Answer 3

"Gesucht ist eine ganzrationale Funktion dritten Grades f(x), deren Graph in P(0|0) die Steigung \(m = \frac{9}{4} \) hat und in Z(9|0) die x-Achse berührt."

\(f(x)=a*x*(x-9)^2\)

\(f´(x)=a*(x-9)^2+a*x*(2x-18)\)

\(f´(0)=a*(0-9)^2=\frac{9}{4}\)    →  \(81a=\frac{9}{4}\) →  \(a=\frac{1}{36}\)

\(f(x)=\frac{1}{36}*x*(x-9)^2\)