auch diese Aussage müsste man erst einmal beweisen, wie soll das gehen? Allgemein kann sie natürlich auch nicht richtig sein, denn manche Funktionen 4. Grades haben ja nur eine Extremstelle. Aber selbst wenn man das beweisen könnte (glaube nicht, dass das richtig ist: Klar, durch Streckung/Stauchung/Verschiebung kriegt man sicherlich einen Extrempunkt zu (0/1), aber warum soll dann automatisch (mit genauer diesem Streckungsfaktor/Verschiebungsfaktor etc.) auch der andere Extrempunkt bei x=2 sein???), verstehe ich immer noch nicht (gesetzt den Fall man könnte zeigen, dass f´´(1) nicht Null sein kann (und das kann man sicher zeigen, da ich ja glaube, dass es NIE möglich ist), was das dann mit der allgemeinen Ausgangsgleichung zu tun hat....wieder hätte man AUSSCHLIESSLICH wieder für eine kleine Teilmenge gezeigt, dass es nicht möglich ist.) Nein, ich denke hier muss man in den sauren Apfel beißen und das unterbestimmte LGS lösen.
Gleichungen f´´(w)=0 (I), f´(w+y)=0 (II) und f´(w-y)=0 (III).
Bei f(x)=ax^4+bx^3+cx^2+dx+e und f´(x)=4ax^3+ebx^2+2cx+d und f´´(x)=12ax^2+6bx+2c führt das dann auch ff. unterbestimmtes LGS:
I: 12w^2*a+6wb+2c=0
II: 4a(w+y)^3+3b(w+y)^2+2c(w+y)+d=0
III: 4a(w-y)^3+3b(w-y)^2+2c(w-y)+d=0
Nun weiter mit binomischer Formel und der dem binomischen Lehrsatz:
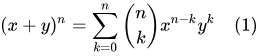
angewandt auf (w+y)^3 (oder etwas mühsamer ohne ihn...:-)).
Wer traut sich? Setzt man übrigens für w und y Zahlen ein, geht das rucki zucki. Es ergibt sich zügig a=0 (z.B. w=2, y=1: Im entstehenden unterbestimmten LGS I-III. Gleichung (um d zu eliminieren, anschließend eine Gleichung mal Minus 2 - addieren und schon steht es da: a=0, was dann schon mal im konkreten Fall heißt, dass es KEINE ganzrationale Funktion 4. Grades geben kann, bei der die Extremstellen bei 1 und 3 liegen und die Wendestelle in der Mitte bei x=2)....