Hallo Mathefrager,
machen wir uns das zunächst einfacher und betrachten zwei Punkte \(A\) und \(B\) in der Ebene. Lässt sich leichter zeichnen und das Prinzip ist dasselbe. $$A= \begin{pmatrix} 1\\ 0 \end{pmatrix}; \quad B = \begin{pmatrix} 3\\4 \end{pmatrix}$$ ich unterstelle, dass Du weißt, was ein Koordinatensystem ist:
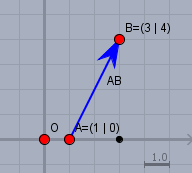
Der rote Punkt \(O\) in der Skizze soll der Ursprung sein, Definitionsgemäß hat dieser die Koordinaten $$O = \begin{pmatrix} 0 \\ 0 \end{pmatrix}$$ Die Koordinaten \((1 \space 0)\) des Punktes \(A\) bedeuten, dass man ausgehend von \(O\) einen Schritt (Kästchen) nach rechts macht und anschließend \(0\) nach oben (also da bleibt!). Dort ist der Punkt \(A\). Genauso geht man bei \(B\) vor. Von \(O\) aus \(3\) Schritte nach rechts und \(4\) nach oben. Markiert man nun den Weg von \(A\) nach \(B\) mit einem Pfeil, so nennt man diesen Pfeil den Vektor \(\vec{AB}\). Einen Vektor kann man genauso mit Koordinaten schreiben, wie einen Punkt: $$\vec{AB} = \begin{pmatrix} ?\\ ? \end{pmatrix}$$ Was sind seine Koordinaten? Wie weit muss ich von \(A\) aus (dort 'startet' der Vektor) nach rechts laufen, damit ich direkt unterhalb von \(B\) lande? Zähle die Kästchen - es sind \(2\). Dann stehe ich bei dem kleinen schwarzen Punkt. Und wie viele Kästchen sind es nach oben bis \(B\)? \(4\) - das war nicht schwer - oder? Also ist $$\vec{AB} = \begin{pmatrix} 2\\ 4 \end{pmatrix}$$ \(2\) nach rechts und \(4\) nach oben. Ausrechnen kann man das auch, indem man beide 'Punkte' subtrahiert: $$\vec{AB} = \begin{pmatrix} 3\\4 \end{pmatrix} - \begin{pmatrix} 1\\ 0 \end{pmatrix} = \begin{pmatrix} 3- 1\\ 4 - 0 \end{pmatrix} = \begin{pmatrix} 2\\ 4 \end{pmatrix}$$ Man rechnet Komponentenweise, d.h. jede Koordinatenrichtung unabhängig von den anderen für sich. Achte darauf, dass der Punkt, zu dem Du hin willst, immer vorn (also positiv) steht. Umgekehrt ist $$\vec{BA} =\begin{pmatrix} 1\\ 0 \end{pmatrix} - \begin{pmatrix} 3\\4 \end{pmatrix} = \begin{pmatrix} 1-3\\ 0-4 \end{pmatrix} = \begin{pmatrix} -2\\ -4 \end{pmatrix} $$ Und das ist genau das negative Ergebnis von vorher. Das ist kein Zufall, denn es gilt immer \(\vec{BA} = - \vec{AB}\); macht doch irgendwie Sinn - oder? Kontrolle am Bild:
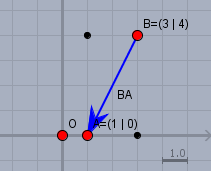
Wie ist der Weg von \(B\) nach \(A\)? Man läuft \(2\) Kästchen nach links (also negativ, da rechts positiv war) und anschließend \(4\) nach unten (wieder negativ, da plus war nach oben!) - macht: $$\vec{BA} = \begin{pmatrix} -2\\ -4 \end{pmatrix} $$ Der Vollständigkeit halber nun der Sprung nach 3D:
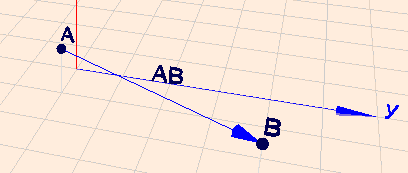
(klick auf das Bild, und drehe die Szene mit der Maus)
Die Rechnung ist genau die selbe wie oben: $$\vec{AB} = \begin{pmatrix} 3\\4 \\1\end{pmatrix} - \begin{pmatrix} 1\\ 0 \\ 1\end{pmatrix} = \begin{pmatrix} 3- 1\\ 4 - 0 \\ 1-1\end{pmatrix} = \begin{pmatrix} 2\\ 4 \\ 0 \end{pmatrix}$$ $$\vec{BA} =\begin{pmatrix} 1\\ 0 \\ 1 \end{pmatrix} - \begin{pmatrix} 3\\4 \\ 1\end{pmatrix} = \begin{pmatrix} 1-3\\ 0-4 \\ 1 \end{pmatrix} = \begin{pmatrix} -2\\ -4 \\ 0\end{pmatrix} $$ wie Du siehst, macht eine Koordinatenrichtung mehr oder weniger keinen grundsätzlichen Unterschied. Alles klar? Frag' nach, wenn Du Fragen hast.
Gruß Werner