Periodenlänge in Abhängigkeit von t berechnen

Question

Ich bin gerade mit meinen Hausaufgaben fertig geworden, wollte euch trotzdem etwas fragen.

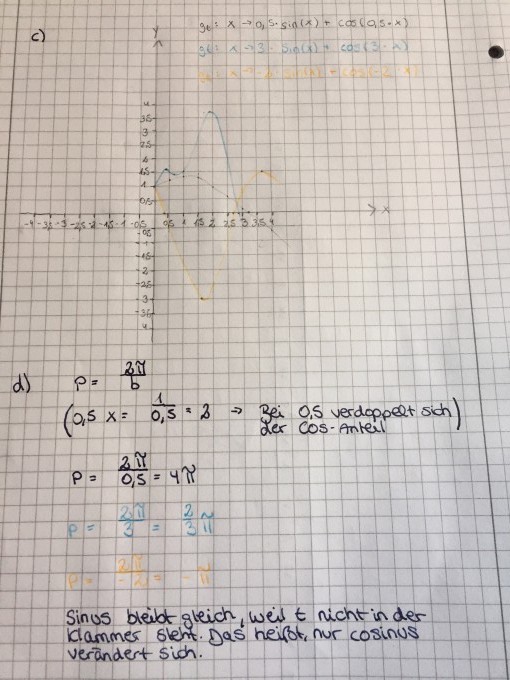
Ich sollte die Periodenlänge der Funktion gut : x —> t*sin(x) + cos(t*x) in Abhängigkeit von t untersuchen.

Ich sollte 3 Graphen skizzieren zu den entsprechenden Funktionen für 3 t-Werte (0,5; 3 und -2)

Ich habe ein Foto hinzugefügt, dort seht ihr auch meine Antwort und meine skizzierten Graphen.

Ich wollte euch fragen, ob ihr mit meiner Antwort „einverstanden“ seit, ob ich etwas falsch gemacht habe oder ob ihr noch etwas hinzufügen würdet!

Ich habe noch eine 2 Frage, die stelle ich aber später  . (Würde hier zu unübersichtlich sein?!)

Würde mich sehr über eure Hilfe freuen! Schönes Wochenende:)

Answer 1

Die Graphen sehen wie folgt aus:

Schwarz=-2 , Grün=3 , Rot=0.5

Ich weiß zwar nicht, was die Aufgabe ist, aber der Sinus bleibt nicht gleich, wenn es einen Vorfaktor gibt. Es ändert sich die Amplitude und der Graph der Sinusfunktion wird in die \(y\)-Richtung gestreckt bzw. gestaucht.

Comments

Okay, danke :)

Ich kann dir ja mal die Aufgebe schicken

---

Du berechnest jeweils die Periode von \(t\sin(x)\) und \(\cos(tx)\) und suchst den kgV.

---

Ich habe wirklich keine Ahnung wie man das macht... Die Periodenlänge von sin(x) und cos(x) ist jeweils 2Pi, aber ich weiß nicht wie das Ergebnis bei t*sin(x) oder cos(t*x) aussieht...

Nehmen wir an t=3 für cos(3x), wäre dann die Periode 2π/3?

Und bei 3*sin(x) auch?

Sorry für die vielen Fragen...

---

Und bei 3*sin(x) auch?

Die Amplitude vom Sinus beeinträchtigt die Periodenlänge nicht. Die Periodenlängen sind:$$P_{\sin(x)}=\frac{2\pi}{1}=2\pi \quad P_{\cos(x)}=\frac{2\pi}{|t|}$$ Nun den kgV suchen:$$kgV\left(2\pi;\frac{2\pi}{|t|}\right)$$ Du kannst dann das für ein paar Zahlen mit \(t∈ℕ\) machen und mal schauen, ob was auffällt.

---

\spoiler

Der Sinus hat immer die Periodenlänge \(2pi\) und der Kosinus \(2\pi/|t|\), was bedeutet, dass der kgV immer \(2\pi\) beträgt.

---

Achso also sind es immer 2Pi?!

Weil ich dachte - wie auf dem Foto zu sehen- es wäre bei 0,5 4 Pi, bei 3 2/3Pi und bei -2 -Pi

Kann es sein, dass es „immer“ 2 Pi ist? Denn bei meiner anderen Frage, die ich hier zu dem Thema gestellt habe, ist es anscheinend ja auch 2Pi...

---

Nein, es ist nicht immer 2π