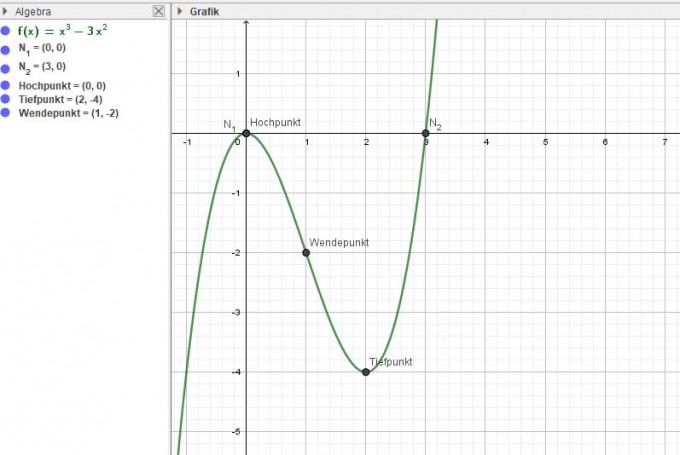
zur Berechnung der Nullstellen setzt du f(x) = 0:
$$x^3-3x^2 = 0$$
und löst nach x auf.
Für die Extremstellen setzt du zunächst die erste Ableitung = 0:
$$3x^2-6x=0$$
und löst wieder nach x auf.
Diese Werte setzt du für x in die zweite Ableitung. Ist das Ergebnis größer als null, handelt es sich um einen Tiefpunkt, ist das Ergebnis kleiner als null, handelt es sich um einen Hochpunkt.
Um die y-Koordinaten der Extrempunkte zu bestimmen, setzt du die x-Werte in die Ausgangsfunktion ein.
Wendepunkte: du setzt die zweite Ableitung = 0 und löst nach x auf:
$$6x-6=0$$
Zu Ermittlung der y-Koordinaten des Punktes/der Punkte setzt du die x-Werte wieder in die Ausgangsfunktion ein.
Eine mögliche Stammfunktion von f(x) ist
$$F(x) = \frac{1}{4}x^4-x^3+c$$