Guten Abend, ich habe ein Problem:
Gegeben war die Menge X := {(x,y) : (x-1)^2 + y^2 = 4} aus dem R^2 und die R^2 -Funktionale
f: R^2 -> R, f(x,y) := 3x^2 - 6x + 2y^2 - 4y + 4.
Hier sollte man das Maximum und Minimum von f auf X bestimmen. Ich hatte die Idee mit der Langrange-Methode. Ich habe folgendermassen angefangen:
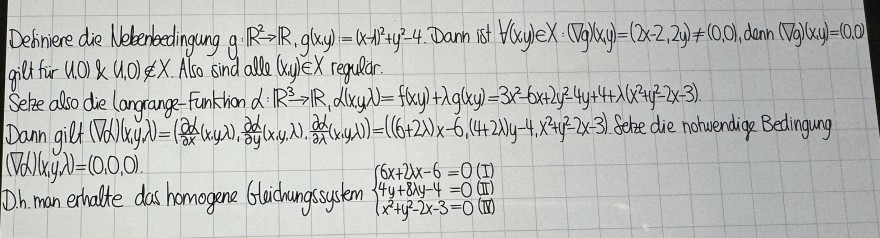
Text erkannt:
Definiere die Nebenledingung \( g \cdot \mathbb{R}^{2} \rightarrow \mathbb{R}, g(x, y)=(x-1)^{2}+y^{2}-4 \). Dann ist \( \forall(x, y) \in X:(\nabla g)(x, y)=(2 x-2,2 y) \neq(0,0) \), denn \( (\nabla g)(x, y)=(0,0) \) gill für \( (1,0) \&(1,0) \notin X \). Also sind all ( \( (., y) \in X \) regular.
Selze also die langrange-Funktion \( \alpha: \mathbb{R}^{3} \rightarrow \mathbb{R}, \alpha(x, y \lambda)=f(x y)+\lambda g(x y)=3 x^{2}-6 x+2 y^{2}-4 y+4+\lambda\left(x^{2}+y^{2}-2 x-3\right) \).
Dann gilt \( (\nabla \alpha)(x, y, \lambda)=\left(\frac{\partial \alpha}{\partial x}(x, y \lambda), \frac{\partial \alpha}{\partial y}(x, y, \lambda), \frac{\partial \alpha}{\partial \lambda}(x, y \lambda \lambda)\right)=\left((6+2 \lambda) x-6,(4+2 \lambda) y-4, x^{2}+y^{2}-2 x-3\right) \). Sebze die notwendige Bedingung \( (\nabla \alpha)(x, y, \lambda)=(0,0,0) \).
D.h. man erhalte das homogene Gleichungssystem \( \left\{\begin{array}{l}6 x+2 x-6=0 \text { (I) } \\ 4+8 y+2 y-4=0(\pi) \\ x^{2}+y^{2}-2 x-3=0 \text { (II) }\end{array}\right. \)
——————————-
Nun ist das Problem mit dem nichtlinearen Gleichungssystem am Ende. Wie löst man soetwas? Das Problem ist ja auch, das dieses nicht schon von Anfang an homogen ist… Ich kann also das Nullproduktkriterium nirgends anwenden :(