Wie viele Rechner in einer Mathe-Klausur? Stochastik, Bernoulli

Question

Die Aufgabe heisst: programmierbare TR dürfen während einer Mathe-Klausur verwendet werden. Die Schüler brauchen diese (im Durchschnitt) für 30 min in 2h. 20 Schüler nehmen an der Klausur teil. Wie viele Taschenrechner sollten zur Verfügung stehen, damit möglichst niemand warten muss (Wahrscheinlichkeit unter 1%)?

Mein Ansatz: Ich müsste die Wahrs berechnen, dass alle Rechner verwendet werden und diese minus 1 Rechben.Die Wahrs. dafür, dass ein TR verwendet wird liegt bei 0,25.

P(X=20) = (20 über 20) * 0,25^20 * 0,75^0 = 9,10 * 10^-13

1-9,10 * 10^-13 = 1

hier komme ich nicht weiter, weil 1 rauskommt... was habe ich falsch gemacht und wie wäre es richtig?

Answer 1

Taste dich an die Antwort ran.

Angenommen, man hat 10 Taschenrechner. Wie groß ist die Wahrscheinlichkeit, dass gleichzeitig 11 bis 20 Rechner gebraucht werden?

Sollte das Ergebnis größer als 1% sein, müssen mind.  11 Rechner da sein.

Falls bei 11 Rechnern die Wahrscheinlichkeit, dass 12 oder mehr Rechner gebraucht werden, immer nach größer als 1% ist,

dann teste ob bei 12 angeschafften Rechnern die Wahrsch für 13 bis 20 benötigte...

Sollte hingegen 10 Rechner schon ausgereicht haben, dann prüfe, ob 9 auch gereicht hätten usw.

Comments

Danke, aber könntest du mir noch bitte sagen wie man das ausrechnet?

---

Das weißt du doch selbst. Du hast mit der richtigen Formel P(X=20) ausgerechnet.

Mit der gleichen Formel musst du P(X=11), P(X=12) ... usw. berechnen und Ergebnisse addieren.

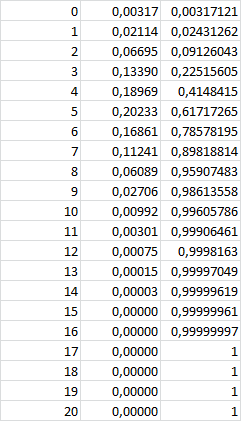
PS: Ich habe mal mit Excel die Wahrscheionlichkeiten, dass 0, 1, 2, ..., 19, 20 TR benötigt werden, ausgerechnet. In der Spalte dahinter ist die kumulierte Wahrscheinlichkeit (Summe der Werte von 0 bis k).

Du siehst, dass die Summe der Wahrscheinlichkeiten für 0 bis 9 Rechner 0,986 ist, und die Summe für 0 bis 10 Rechner 0,996 ist.
9 Rechner genügen also nur mit 98,6%-iger Sicherheit, während 10 Rechner mit 99,6-prozentiger Sicherheit reichen. Also ist erstmals bei 10 Rechnern das Risiko kleiner als 1%.