Berechne Basis des Kerns, Basis des Bildes einer lienaren Abbildung Q4 → Q3.

Question

Aufgabe:

Berechne eine Basis des Kerns und des Bildes der linearen Abbildung ℚ⁴ → ℚ³,
die durch Linksmultiplikation mit der folgenden Matrix definiert ist: 

A = \( \begin{pmatrix} 2 & 1  & -1 & 2 \\ 1 & 0  & -1 & 0 \\ 3 & 1  & -2 & 2 \end{pmatrix} \)

Ansatz:

Gesucht:

Basis des Kerns (von was?)
Basis des Bildes (von was?)

Was ist gegeben?
Eine lineare Abbildung ℚ⁴ → ℚ³. 

Erste Idee für den Kern:

A ist aus ℚ³ weil es 4 Vektoren mit jeweils 3 Zeilen aufweist. 
Das heisst, für die Berechnung des Kerns muss ich A von links her mit einer Matrize B multiplizieren, damit es 
dann als Matrixprodukt den Nullvektor oder die Nullmatrize ergibt. 
Da A (ich vermute aus ℚ³  ist) muss der Vektor/Matrize B drei Spalten haben, weil B (ich vermute aus ℚ⁴ ist, hat B 4 Zeilen. 

Frage zu meiner Idee
Das heisst also, für den Kern muss ich folgendes tun:

B*A = 0v

wobei B(4x3) und A(3x4) ist und 0v wird (4x4 sein) 

Lösungsvorschlag:

B*A = \( \begin{pmatrix} a1 & b1  & c1 \\ a2 & b2 & c2 \\ a3 & b3 & c3 \\ a4 & b4 & c4  \end{pmatrix} \) * \( \begin{pmatrix} 2 & 1  & -1 & 2 \\ 1 & 0  & -1 & 0 \\ 3 & 1  & -2 & 2 \end{pmatrix} \) = 0v

Wenn ich das gelöst habe, weiss ich, was der Kern, also in diesem Fall ist der Kern B, ist. Wenn ich den Kern habe kann ich dort die linear abhängigen eliminieren und dann habe ich die Basis des Kerns. 
Erst dann fahre ich fort zum Bild und nehme dann die Basis vom Bild. 

Frage zum Problem wie ich es löse
Das aber auszurechnen gibt mir pro Spalte jeweils viel zu viele LGS.

Wie kann ich das lösen ?
Ich bin um jede Hilfe dankbar ! 



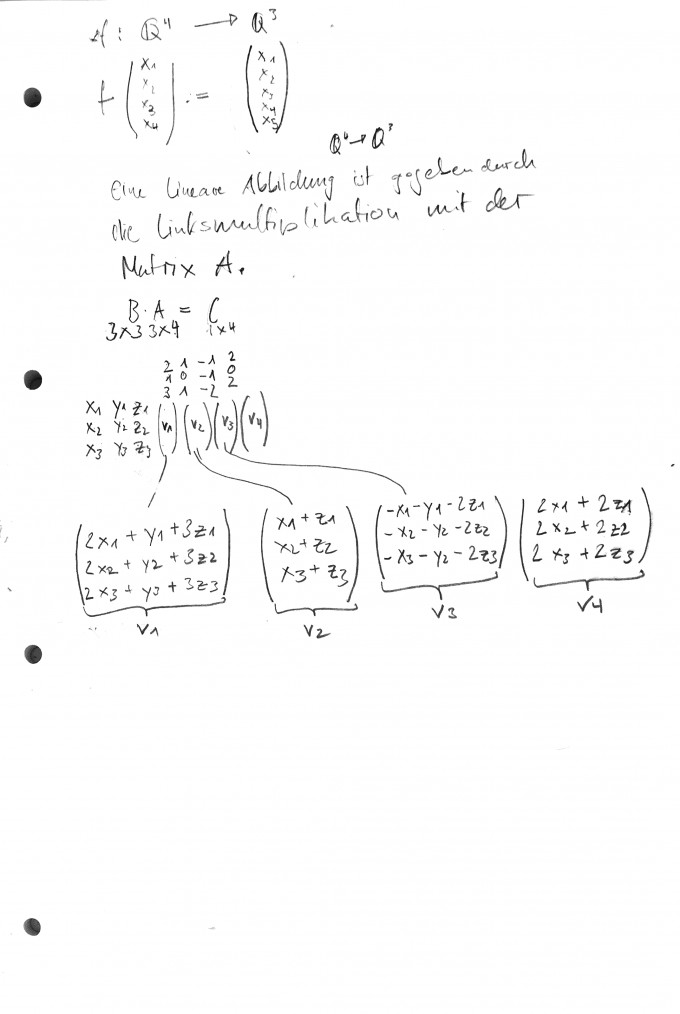
Was ich bis jetzt habe: (Zur evaluierung der Abbildung an sich):

Answer 1

Vielleicht solltest Du Dein Grundlagenwissen auffrischen?

Kern Q^4↦Q^3 ===> A x =0

A ist eine 3x4 Matrix

A+Gaussalg. bis zur Treppenstufenform A_D

\(A_D\cdot x \, =  \, \left(\begin{array}{rrrr}1&0&-1&0\\0&1&1&0\\0&0&0&1\\\end{array}\right) \cdot x\) = 0

===> \({x1 = , x2 = , x3 = t ,x4=}\)

Comments

Danke für die Antwort ! 

Vielleicht solltest Du Dein Grundlagenwissen auffrischen?

Ganz bestimmt ! Ich bin eher am Auffrischen als dass ich am Studium richtig teilnehme. 

A+Gaussalg. bis zur Treppenstufenform A_D

Heisst das, dass ich direkt auf die Matrix den Kern und das Bild bestimmen kann und nacher zur Basis gelange ? ODer heisst das, dass ich A + Gaussalgor. von irgendeiner andere Matrix anwenden muss. 

Mein zweiter Versuch bis bevor ich deine Antwort gelesen habe:
Kannst du noch sagen ob ich mit meiner Idee unten völlig aufm Holzweg bin ? 

---

Ich versteh Deinen Gedankengang nicht wirklich:

Der Kern ist der Vektorraum, der auf den 0-Vektor abgebildet wird

===> löse: A x = 0

x=0 ist die triviale Lösung: der 0-Vektor (R^4) \(\left(\begin{array}{r}0\\0\\0\\0\\\end{array}\right)\)wird auf den 0-Vektor R^3 \(\left(\begin{array}{r}0\\0\\0\\\end{array}\right)\) abgebildet - Du suchst nun noch weitere Teilnehmer an der Party...

---

Ich versteh Deinen Gedankengang nicht wirklich:

In der Aufgabe ist gesucht:
- die Basis des Kerns. 
- die Basis des Bilds. 

Aber von was? 
Laut Text von der lin. Abbildung die gegeben ist durch die Linksmultiplikation mit der Matrix A. Aber was ist die lin. Abbildung? ODer ist es tatsächlich einfach von nur der Kern der Matrix A? 


Von was ich Kern und Bild berechnen muss weiss ich nicht ganz genau, aber wie man Kern und Bild herausfindet, habe ich durch Auffrischen an einem Beispiel einer 2x2-Matrix herausgefunden.

Kern: 
Zuerst prüft man mit der Determinante ob ein Kern existiert. 
Dann Multipliziert man die Matrix mit einem Vektor und das soll Null ergeben, dieser Vektor, der zum Ergebnis Null führt, ist dann der Kern der Matrix.

Kern in dieser Aufgabe:
Hier in dieser Aufgabe habe ich allerdings eine 3x4 Matrix und ich denke, dass der Vektor dann durchaus mehrspalitg sein kann also möglicherweise eine Matrix ist und eben deren Multiplikation also Matrixprodukt soll 0v, 0v könnte in dieser Aufgabe ebenfalls mehrspaltig sein. 

Mein Problem ist,
dass ich nicht sehe was die Abbildung ist und deswegen viel herumprobiere und nach dem herumprobieren habe ich hier im Forum gefragt. 

Bild: 
Das Bild ist ähnlich wie die Wertemenge bei einer Funktion oder Abbildungen. Also eine Lösungsmenge oder Span. 

Ich hoffe dass mein Problem jetzt klarer zu verstehen ist. :-/

---

Ok ich bin schon einen Schritt näher. 

Ich habe jetzt herausgefunden was die Abbildung ist: 

Ich gehe davon aus, dass der Kern der Matrize die aus dem Matrixprodukt A*x entstanden ist gesucht ist, und wenn ich den Kern habe, kann ich dessen Basis berechnen. 

Und das Bild lässt sich dann auch herausfinden. 

Hier ein Bild meines Fortschritts:

---

Ja, stimmt, eine Annäherung ;-).

Obwohl ich es ober schon geschrieben habe. Um den Kern von f, wie Du die Abb genannt hast, zu bestimmen löse das GLS

A x = 0

so, wie Du es aufgeschrieben hast.

Kern:
Zuerst prüft man mit der Determinante ob ein Kern existiert.
Dann Multipliziert man die Matrix mit einem Vektor und das soll Null ergeben, dieser Vektor, der zum Ergebnis Null führt, ist dann der Kern der Matrix.

Die Lösung hab ich ebenfalls aufgeschrieben und A_D (entsteht, wenn man den Gaussalg. auf A anwendet) genannt.

---

Voelen Dank, deine Antwort ist super, vielleicht werde ich aber trotzdem noch rückfragen müssen. :-)

---

Wenn Fragen bleiben, bittte und Danke...

Rein Sprachlich: Eine Matrix hat keinen Kern - hört man aber immer wieder. Bei einer linearen Abbildung spricht man von einem Kern - eben dem Vektorraum der auf den 0-Vektor abgebildet wird..