Aufgabe:
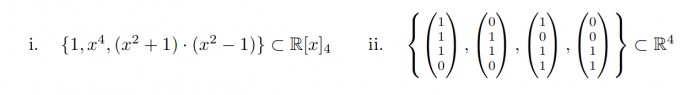
Problem/Ansatz:
Ansatz zu der i):
a*1 + b*x^4 +c*( (x^2 +1) * (x^2 -1)) = 0
a*1 + b*x^4 + c*(x^4 -x^2 + x^2 -1) = 0
a*1 + b*x^4 + c*x^4 -1*c = 0
a*1 + (b+c)*x^4 -1*c = 0
=> Wie kann ich nun zeigen, das es nur die triviale Lösung a=b=c=0 gibt oder geht dies schon aus der Gleichung hervor?
R[x]4={ax4+bx3+cx2+dx+e:a,b,c,d,e∈R}