Hallo Roland,
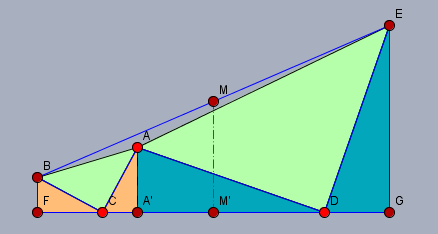
Ich habe noch zwei weitere Punkte eingezeichnet. \(A'\) ist der Lotpunkt von \(A\) auf \(CD\) und \(M'\) der Lotpunkt von \(M\) auf \(CD\). Die bräunlichen Dreiecke \(\triangle ACA'\) und \(\triangle CBF\) sind kongruent, da sie in allen Winkeln und einer Seite (\(|AC| = |CB|\)) übereinstimmen. Gleiches gilt für die beiden kongruenten blauen Dreiecke \(\triangle EDG\) und \(\triangle DAA'\). Da \(M\) der Mittelpunkt von \(BE\) ist, muss gelten: $$|MM'| = \frac12(|BF| + |GE|)$$ Nun ist aber wegen der kongruenten Dreiecke $$|BF| = |CA'|, \quad |GE| = |A'D|$$ Einsetzen in die Gleichung für die Mittelparalelle $$|MM'| = \frac12 (|CA'| + |A'D|) = \frac12 |CD|$$ BTW.: da $$|FC| = |A'A| = |DG|$$ ist \(M'\) auch der Mittelpunkt von \(CD\). Gruß Werner