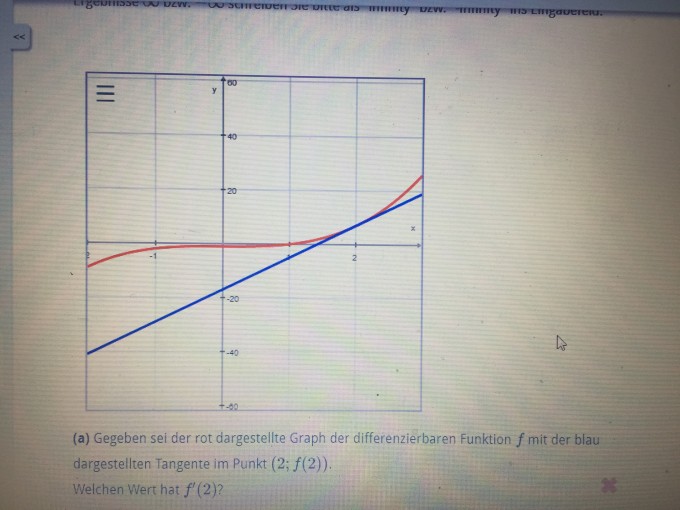
Aufgabe: Gegeben sei der rot dargestellte Graph der differenzierbaren Funktion f mit der blau
dargestellten Tangente im Punkt (2;f(2)).
Welchen Wert hat f′(2)?
Problem/Ansatz:
Habe im Anhang ein den Graph hochgeladen.
Komme bei der Aufgabe nicht weiter. Mein Problem ist, dass ich zwar Tangentenfunktionen berechnen kann, aber mir noch die entscheidende Idee fehlt, wie ich auf f´(2) komme.
Wenn man die Funktion als Gleichung gegeben hätte, wüsste ich was ich machen muss. Wir haben aber leider nur den Graph mit der Funktion und seine Tangente an Punkt x=2.
Wer kann mir ein Tipp geben?