Geben Sie alle Häufungspunkte der Folgen an und Teilfolgen von (an)

Question

Berechnen Sie die Grenzwerte folgender Zahlenfolgen falls existent. Geben Sie alle Häufungspunkte der Folgen an und Teilfolgen von (a_n), die gegen lim sup_n→∞ a_n bzw. lim inf_n→∞ a_n konvergieren.

$$ an = (1 + \frac{1}{2n} )^{3n} $$

Mein Ansatz:

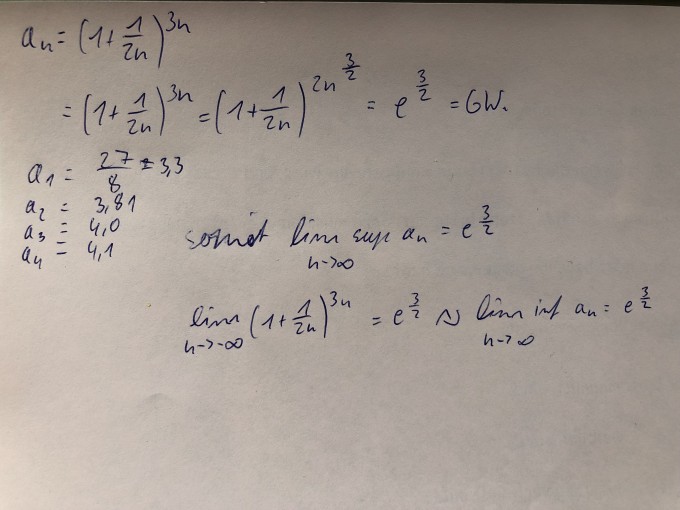
Komme allgemein mit dem Thema gerade überhaupt nicht richtig zurecht, ich habe jetzt einmal für ∞ und -∞ die Grenzwerte ermittelt und jeweils e^^{\( \frac{3}{2} \)}  ermittelt, demzufolge lim sup an = e^^{\( \frac{3}{2} \)} und lim inf an = e^^{\( \frac{3}{2} \)} ist das gemeint? Freue mich über eure Hilfe!^^

Answer 1

Bei Zahlenfolge gibt es bei der Grenzwertbetrachtung immer

nur den Fall   n gegen ∞ .

Da deine Folge ja gegen e^(3/2) konvergiert, hast du für

alle drei Grenzwerte  lim  = lim sup   = lim inf   =  e^(3/2)

siehe auch https://de.wikipedia.org/wiki/Limes_superior_und_Limes_inferior#Eigenschaften