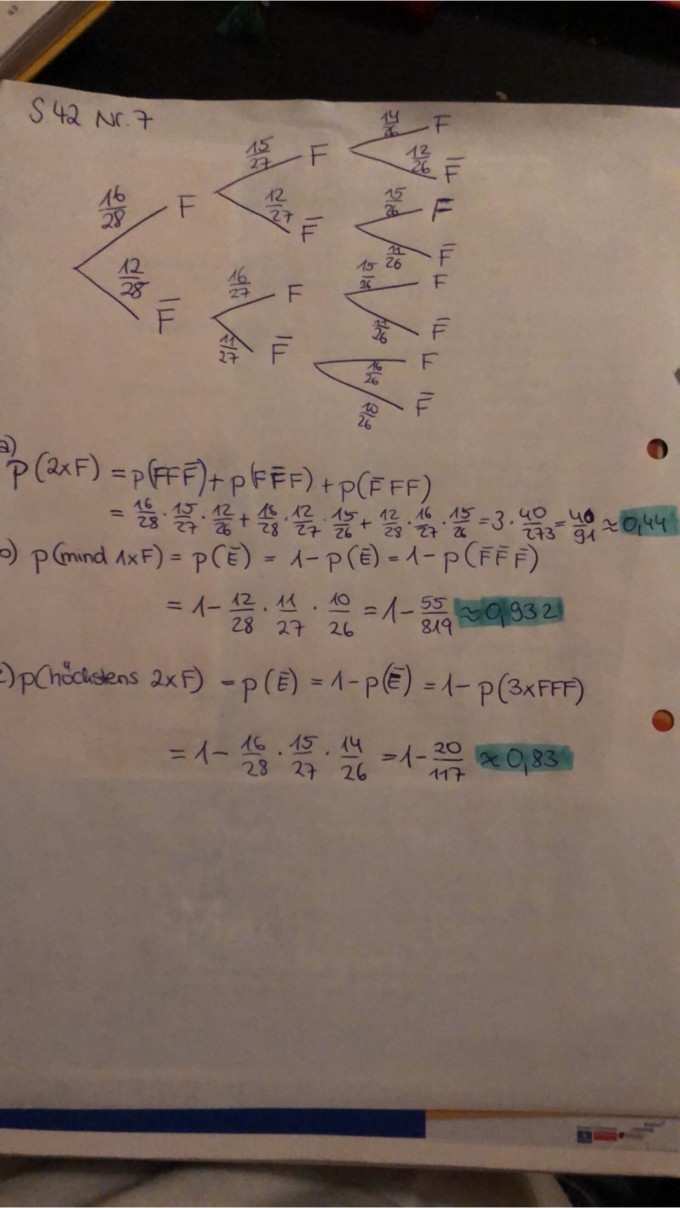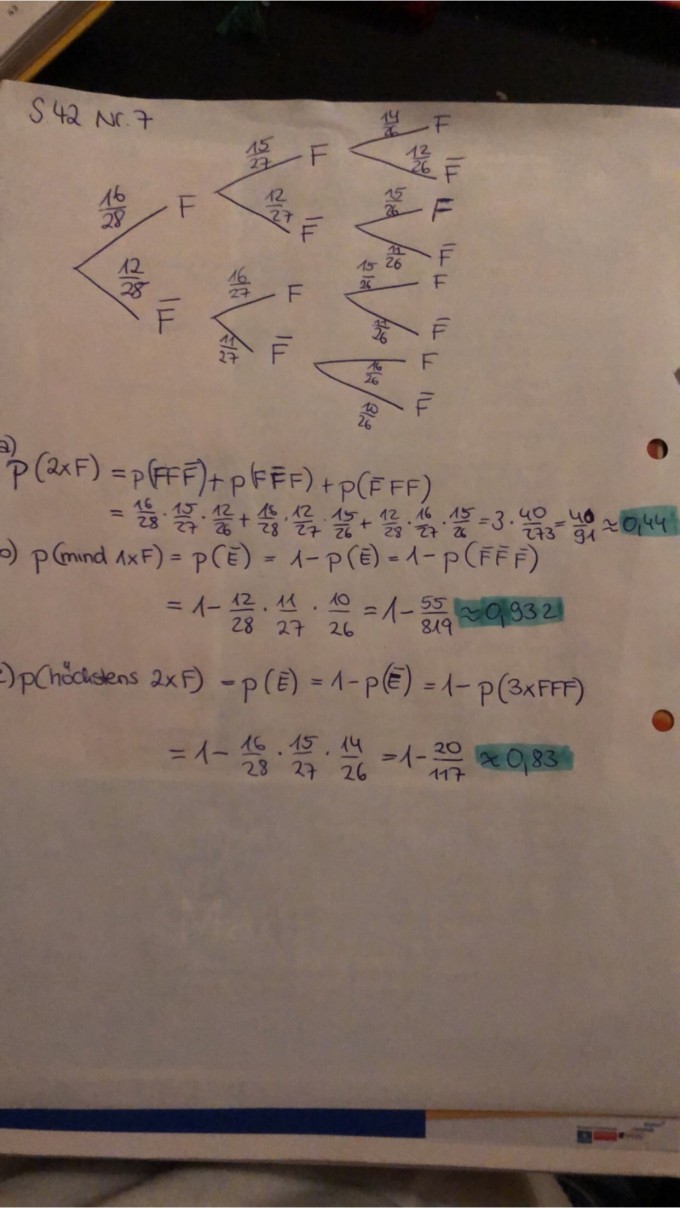Aufgabe:
Von den 28 Schülerinnen und Schülern der 8a kommen 16 mit dem Fahrrad zur Schule. Berechne die Wahrscheinlichkeit, dass von drei zufällig ausgewählten Schülern
a) genau zwei mit dem Fahrrad kommen
b) mindestens einer mit dem Fahrrad kommt
c) höchstens zwei mit dem Fahrrad kommen.
Problem/Ansatz:
s. Foto