Steckbriefaufgabe: Symmetrisch zu (0|0) und Minimum bei (-2, -4)

Question

Welche Polynomfunktion dritten Grades besitzt einen Graphen der symmetrisch ist zum Nullpunkt und in p(-2/-4) ein relatives Minimum annimmt? Die erste Bedinngung welche ich gefunden habe ist f''(-2)=-4 , doch bei der und den anderen bin ich mir nicht sicher... Bitte um Hilfe

Answer 1

Welche Polynomfunktion dritten Grades besitzt einen Graphen der symmetrisch ist zum Nullpunkt

f(x) = ax^3 + bx

und in p(-2/-4) ein relatives Minimum annimmt? 

f(-2) = -4

f'(-2) = 0

 

f(x) = - 1/4·x^3 + 3·x

Comments

Ich verstehe diese Funktion nicht f(x) = ax3 + bx    wie kommt man auf diese?

---

Symmetrie bezügl. Ursprung heisst ja 'ungerade Funktion'.

Da kommen in der Funktionsgleichung nur ungerade Exponenten von x vor.

Also von Vornherein: 0x^2 und 0.

---

ahhh oke danke =)

aber wie komme ich jetz auf die anderen drei Bedingungen ausser f(-2)= -4 ?

---

aber wie komme ich jetz auf die anderen drei Bedingungen ausser f(-2)= -4 ?

Du hast ja nur 3 Unbekannte in y = ax^3 + bx.

Also genügt eine weitere Bedingung.

Unknown hat sie dir schon angegeben:

 

f'(-2) = 0           (Bedeutung: Steigung im Minimum ist 0)

Answer 2

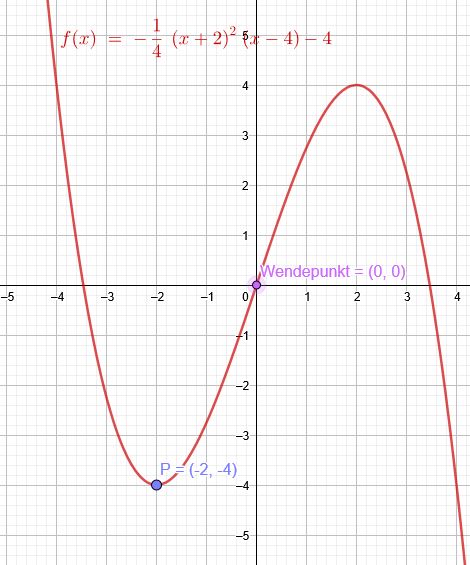
"Welche Polynomfunktion dritten Grades besitzt einen Graphen der symmetrisch ist zum Nullpunkt \(N(0|0)\) und in \(P(-2|-4)\) ein relatives Minimum annimmt?"

Ich verschiebe den Graphen von \(f(x)\) um 4 Einheiten nach oben: doppelte Nullstelle in \(P´(-2|0)\)

\(f(x)=a*(x+2)^2*(x-N)\)

\(N(0|0)\)→ \(N´(0|4)\)

\(f(0)=a*(0+2)^2*(0-N)=-4*a*N=4\)    \(a=-\frac{1}{N}\)

\(f(x)=-\frac{1}{N}*[(x+2)^2*(x-N)]\)

\(N´(0|4)\) ist auch Wendepunkt:

\(f´(x)=-\frac{1}{N}*[(2x+4)*(x-N)+(x+2)^2]\)

\(f´´(x)=-\frac{1}{N}*[(2)*(x-N)+(2x+4)+(2x+4)]\)

\(f´´(0)=-\frac{1}{N}*[(2)*(0-N)+(4)+4]\)

\(-\frac{1}{N}*[-2N+8=0\)    \(N=4\)   \(a=-\frac{1}{4}\)

\(f(x)=-\frac{1}{4}*(x+2)^2*(x-4)\)

\(p(x)=-\frac{1}{4}*(x+2)^2*(x-4)-4\)