Ich vermute, dass du folgendes meinst:
(-3)^4=+81 ist richtig, während du falsch mit -3^4=-81 rechnest.
Die Vorzeichen müssen bei negativen x-Werten deshalb abwechselnd + und - sein.
--------
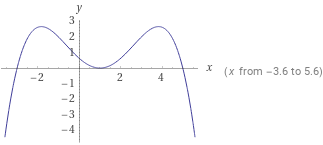
Wenn Nullstellen vorgegeben sind, kann man mit Linearfaktoren einfacher rechnen.
f(x)=a(x+3)(x-1)²(x-b)
Offensichtlich gilt noch f(3)=2 und f(-1)=2
2=a•6•2²•(3-b) → 2=24a•(3-b)
2=a•2•(-2)²(-1-b) → 2=8a•(-1-b) (*)
Nun dividiere ich beide Gleichungen.
1=3(3-b)/(-1-b)
(-1-b)=9-3b--> b=5
Einsetzen in (*)
2=8a•(-6) --> a=-1/24
f(x)= -1/24 •(x+3)(x+-1)²(x-5)
\( f(x)=-\frac{x^{4}}{24}+\frac{x^{3}}{6}+\frac{5 x^{2}}{12}-\frac{7 x}{6}+\frac{5}{8} \)