Was ist nun der Grenzwert

Question

Aufgabe:

Es ist nicht die Aufgabe aber ich will etwas aufgrund der verständnis klären.

Problem/Ansatz:

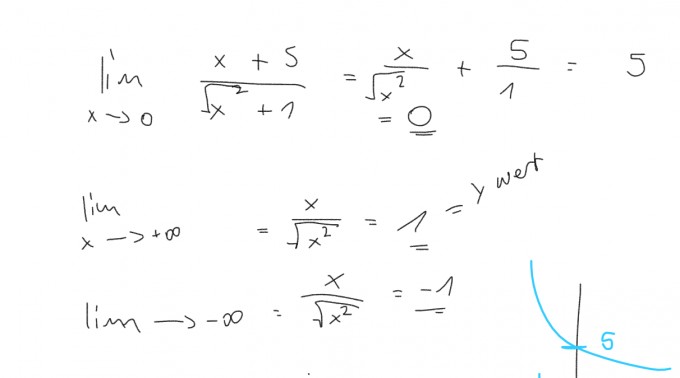
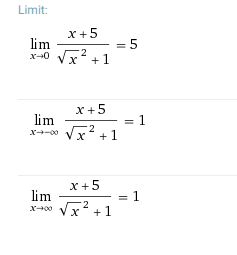
So wie ich es verstehe werden für x gegen unendlich die Werte von 1 bis unendlich eingesetzt daher verstehe ich das gleich 1 rauskommt, aber wenn ich x gegen minus unendlich laufen lasse sollte doch -1 rauskommen, da die Werte -1 bis minus undendlich genommen werden.

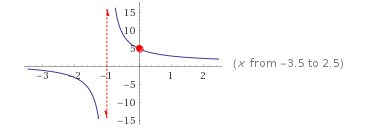
Und wenn beide Grenzwerte laut Limit 1 sind warum wird hier jetzt gezeigt das beide gegen -1 laufen?

Comments

Du hast bei der Eingabe die Klammer um x^2 vergessen.

Answer 1

Da ist ein Fehler in der Lösung. -1 ist richtig.

Comments

Ok Gut zu wissen dann das ich mich nicht immer auf Wolfram Alpha verlassen kann ^^

---

Das kannst dir hier durchaus:

https://www.wolframalpha.com/input/?i=lim+(x%2B5)%2F((x%5E2)%5E0.5%2B1))

---

achso ok ich hab nämlich das Wurzel symbol benutzt, aber wenn es so dann besser klappt.. Danke :)

---

Deine Bruchzerlegung ist kriminell! :)

Es gilt:

(a+b)/(c+d) = a/(c+d)  + b/(c+d)

---

Ja stimmt Danke für die Korrektur :D

Answer 2

Wenn das so richtig dargestellt ist: (x+5)/(√(x²)+1),dann ist √(x²)=|x| und für x>0 einfach x.

Die Umformung (x+5)/(√(x²)+1)=x/√(x²)+5/1 ist falsch. Auch die Vermutung _x→0lim[x/√(x²)] =0 ist falsch. Zufällig heben sich beide Fehler gegenseitig auf, sodass der Grenzwert richtig wird.

Answer 3

Lautet der Term des Nenners \(\sqrt{x^2}\) oder \(\sqrt{x}^2\)?

Comments

√x^2 also das erste :D hat sich aber schon geklärt

---

Alles klar, immer schön daran denken, die sqrt() Klammer um alles zu setzen ;)

---

wenn du dich auf die 2. Grafik beziehst so hat das Web-Programm es geschrieben ^^

---

  Es kommt halt darauf an, wie man es schreibt.