Eine Pyramide hat eine quadratische Grundfläche: Höhe ausrechnen

Question

Eine Pyramide hat eine quadratische Grundfläche. Die Länge einer Grundflächenkante berträgt 80m,die Länge einer Kante von einer Ecke der Grundfläche bis zur Spitze der Pyramide bertägt 60m. Wie hoch ist die Pyramide?

Answer 1

Es gilt nach dem Pythagoras

s^2 = (a/2)^2 + (a/2)^2 + h^2
s^2 = 1/2 a^2 + h^2

Auflösen nach h ergibt

h^2 = s^2 - 1/2 a^2
h = Wurzel(s^2 - 1/2 a^2) = Wurzel(60^2 - 1/2*80^2) = 20 m

Die Pyramide ist 20 m hoch

Comments

wieso denn 2 mal  1/2 a ^2 ??

---

(a/2)^2 + (a/2)^2 ist ein Ausdruck auch nach dem Phythagoras welche die länge der halben Diagonale der Grundseite beschreibt.

Die halbe Diagonale bildet ja mit Seitenkante und Höhe ein rechtwinkliges Dreieck.

(a/2)^2 + (a/2)^2 = (d/2)^2 und

s^2 = (d/2)^2 + h^2

Also

s^2 = (a/2)^2 + (a/2)^2 + h^2

---

kannst du mir eine skizz machen damit ich es besser verstehen kann?

---

Skizze nachgereicht:

Eigene Pyramiden erstellen (und Berechnungen durchführen) mit:
https://www.matheretter.de/rechner/pyramide

Für Berechnungen an Pyramiden siehe auch Videos auf:
https://www.matheretter.de/wiki/pyramide/

Answer 2

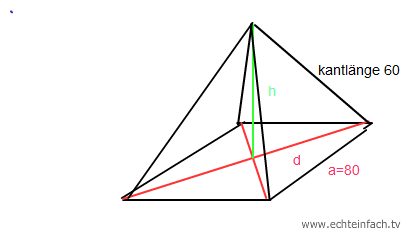
Um die Höhe zu berechnen , braucht man die Hälfte der Diagonale der Grundfäche , im Prinzip muss man zweimal den Pyrthagoras anwenden.Einmal für die Diagonale , und für die Höhe.

gegeben  a=80 und Kantlänge  =60

d/2=(√80²+80²)/2

      =56,56

die Höhe ist dann:

h=√60³-56,56²

   = 20,0007 

Die Pyrfamide ist dan ungefähr 20m hoch.

siehe Skizze