Wie gehe ich hier mit dem Sinussatz um?

Question

Aufgabe: Berechne jeweils die fehlenden Seiten und Diagonalenlängen sowie Winkel in einem Parallelogramm ABCD.

a) b = 16,1 cm ; c = 44,2 cm ; Gamma = 99 grad.

Problem/Ansatz:

Ich habe hier den Sinussatz angewendet. Weiß aber nicht wie ich ihn hier umstelle. Kann man mir bitte helfen? Ich freue mich für eine ausführliche Erklärung.

Answer 1

SIN(β)/16.1 = SIN(99°)/44.2

β = SIN^(-1)(SIN(99°)/44.2*16.1) = 21.09°

Nun den dritten Winkel und danach die dritte Seite bestimmen.

Comments

Ich habe das so eingegeben komme aber nicht auf auf das Ergebnis.

Answer 2

Für mich stellt sich das Parallelogramm so dar:

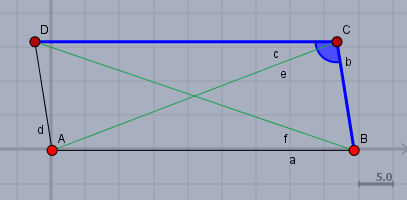
Die blauen Seiten und der blaue Winkel sind gegeben. Die weiteren Seiten und Winkel sind trivial: $$a = c = 44,2 \text{cm} \\ d = b = 16,1 \text{cm} \\ \alpha = \gamma = 99° \\ \beta = \delta = 180°-\gamma = 81°$$ und die Diagonalen lassen sich mit Hilfe des Kosinussatz berechnen: $$e = \sqrt{a^2 + b^2 - 2ab \cos \beta} \approx 44,61 \text{cm} \\ f =  \sqrt{d^2 + a^2 - 2da \cos \gamma} \approx 49,35 \text{cm}$$