(1) Mit dem Arithmetischen Mittel, die Mitte der Diagonale bestimmen:$$M\left(\frac{x_{1}+x_{2}}{2};\frac{y_1+y_2}{2}\right) \Longrightarrow M\left(7;5\right)$$
(2) Funktion aufstellen für die Strecke:
\(A(1|3) \quad C(13|7)\)$$f(x)=\frac{y_2-y_1}{x_2-x_1}(x-x_1)+y_1$$$$f(x)=\frac{1}{3}x+\frac{8}{3}$$
(3) Orthogonale Funktion aufstellen (negative reziproke Steigung):$$g(x)=mx+n ,\quad m=-\frac{1}{m_f}$$$$g(x)=-3x+n$$
(2b) Mittelpunkt verwenden:$$5=-3\cdot 7+n \quad \Longrightarrow n=26$$$$g(x)=-3x+26$$
Auf dieser Gerade müssen nun zwei Punkte liegen, deren Abstand die Hälfte des Abstands von \(AB\) beträgt.
(3) Abstand von AB berechnen:$$\Delta_{AB}=\sqrt{(y_2-y_1)^2+(x_2-x_1)^2}$$$$\Delta_{AB}=\sqrt{(7-3)^2+(13-1)^2}$$$$\Delta_{AB}=4\sqrt{10}$$
Der gesuchte Abstand ist also \(\frac{\Delta_{AB}}{2}=2\sqrt{10}\).
(4) Kreisgleichung mit \(r=\sqrt{10}\) am Mittelpunkt:
Die allgemeine Kreisgleichung mit gegebenen Mittelpunkt ist \((x-x_0)^2+(y-y_0)^2=r^2\). Daraus folgt:$$(x-7)^2+(y-5)^2=10$$
(4b) Nach \(y\) umstellen:$$(x-7)^2+(y-5)^2=10$$$$(y-5)^2=10-(x-7)^2 \quad |\pm\sqrt{}$$$$y=\pm\sqrt{10-(x-7)^2}+5$$ Das sind zwei Gleichungen, die du mit \(g(x)\) gleichsetzt, um die \(x\)-Koordinanten der Punkten zu berechnen.
(4c) Schnittpunkte berechnen:
Du musst nur die Schnittpunkte einer Funktion berechnen, da du beim Prozess der Bestimmung der Nullstellen quadrierst! Such dir also eine aus:
$$\sqrt{-x^2+14x-39}+5=-3x+26$$$$\sqrt{-x^2+14x-39}+5=-3x+26 \quad |-5$$$$\sqrt{-x^2+14x-39}=-3x+21 \quad |\uparrow ^2$$$$-x^2+14x-39=(-3x+21)^2$$$$-x^2+14x-39=9x^2-126x+441$$$$-10x^2+140x-480=0 \quad |:(-10)$$$$x^2-14x+48=0$$$$(x-6)(x-8)=0 \quad \Longrightarrow x_1=6 \quad \vee \quad x_2=8$$
Du kannst hier bereits aufhören. (Man hat beide Lösungen, weil quadriert wurde) Die Punkte errechnest du, indem du \(x_1\) und \(x_2\) ihrem \(y\)-Wert zuschreibst, indem du in die Funktion \(g(x)\) einsetzt!$$g(8)=2 \quad ; \quad g(6)=8$$ Die Punkte lauten also \(P(8|2)\) und \(Q(6|8)\)
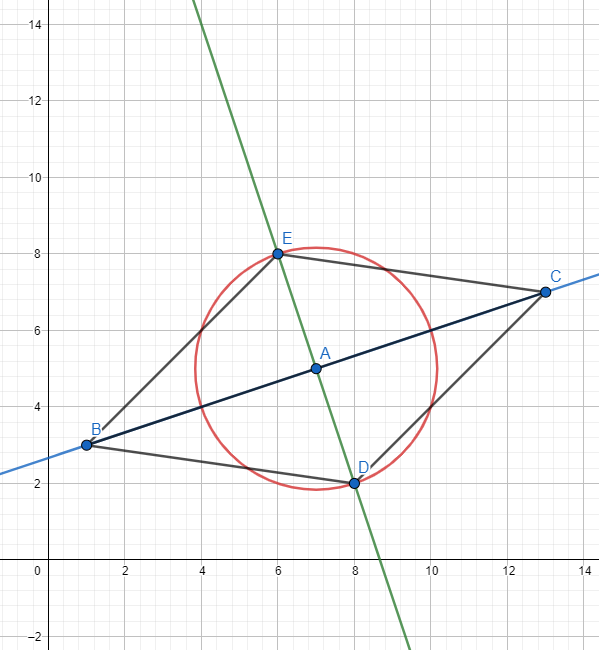
Nun einfach nur noch die Punkte verbinden - dann hast du die Raute!
Fertig sieht es so aus: