Abstand zweier gegebenen Funktionen, wo der Höhenabstand der Funktionen identisch ist

Question

liebe Community,

Aufgabe:

Ich soll überprüfen, ob der Abstand der gegebenen Funktionen f(x) und g(x) mindestens 2LE ist. Die Funktionen sind:
f(x) = \( \frac{x^{3}}{9} \) - \( \frac{x}{3} \)
g(x) = \( \frac{x^{3}}{9} \) - \( \frac{x^{2}}{9} \) - \( \frac{x}{3} \) + 1

Die beiden Funktionen geplottet sehen wie folgt aus (Definitionsbereich: -3, 3):

f(x) = blau

g(x) = lila

Problem/Ansatz:

Mein Ansatz war, zwei Tangenten bei x=0 zu finden. Mit Hilfe dieser Tangenten wollte ich somit schon mal die Höhe "absichern", da ja nach dem Abstand der Funktionen bei identischer Höhe gefragt wird (rote Linien in der Skizze). Jetzt muss man also die Punkte finden, an denen sich die Steigung ändern (blaue x in der Skizze). Damit kann man dann jeweils die ⊥-Funktion finden kann (grüne gestrichelte Linien). Damit würde ich den Abstand begrenzen. Schlussendlich muss man dann nur noch den Abstand der zwei "Begrenzungsgeraden" finden (lila gestrichelte Linie in Skizze) und das Ergebnis überprüfen, ob es größer gleich 2LE ist. In Theorie ist das alles machbar, aber ich komme an einer kleinen Stelle einfach nicht weiter. Skizzen zur Verdeutlichung folgen:

Gerade g₁(x) an Funktion f(x):

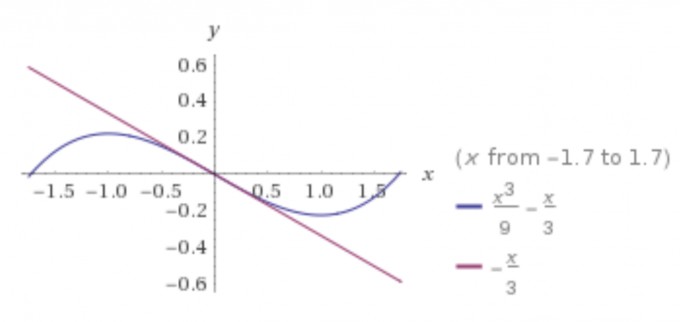
Gerade g₂(x) an Funktion g(x):

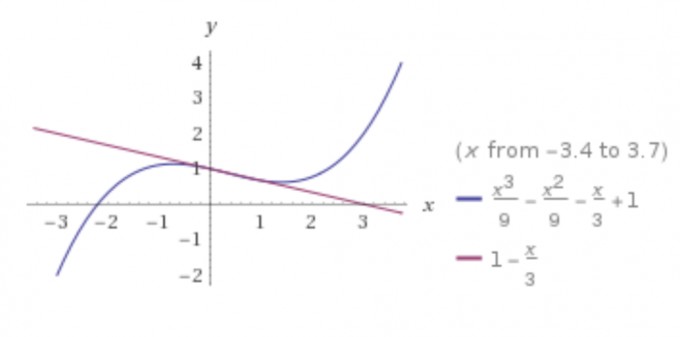
Skizze zur Veranschauung meines Vorgehens:

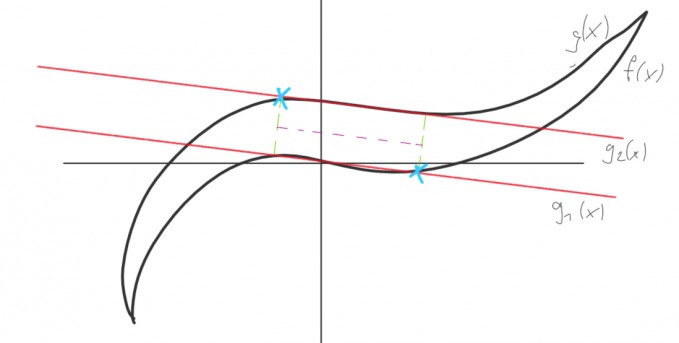
Jetzt zu meiner Frage:

Wie finde ich die Punkte, wo die Funktionen die Steigung dann ändern (blaue x in der Skizze) ? Oder soll ich gar einen anderen Weg versuchen? Wenn ja, dann bitte welchen. Ich hätte keine Ahnung was noch gehen könnte.

Mit freundlichen Grüßen

Comments

Du meinst beim Intervall [-3,3] sicherlich den Definitionsbereich und nicht den Wertebereich, oder?

Answer 1

Wenn ich dich richte verstehe, willst du wissen, wo die zwei Geraden den größten Abstand zu einander haben.

Du sieht in dem Graphen schon, dass dies vermutlich bei x=0 sein wird und ca. 1LE ist.

subtrahiere die beiden Funktionen doch voneinander. Dann hast du die Differenzwerte.

\(\rightarrow h(x)=g(x)-f(x)=1-\dfrac{x^2}{9}\)

Dann suchst du ein Maximum (der Abstand soll ja maximal sein). Also h'(x)=0

Das wäre doch ein Anfang, oder?

Answer 2

Ich vermute, dass es um den Abstand der beiden Wendepunkte geht also (0|0) und (1/3|214/243).Dieser Abstand ist ungefähr 0,94163.