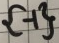Könnt ihr mir vielleicht bei der Aufgabe helfen, bzw. den Ansatz erklären.
:))
Lineare Algebra. f((x1, x2, x3)) := 2x_1 - x_2 + 3x_3. Elemente von R^3 mit f^(-1)({1}) = x + < {y,z} > ?
Die lineare Abbildung \(f: \space \mathbb{R}^3 \to \mathbb{R}\) sei definiert durch $$f\left( \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}\right) := 2x_1 - x_2 + 3x_3$$Bestimmen Sie Elemente \(x,y,z \in \mathbb{R}\) mit \(f^{-1}( \{\colorbox{#ffff00}{?} \}) = x + \left< \{y,z\}\right>\).
Geben Sie zusätzlich die Ebene \(f^{-1}( \{ \colorbox{#ffff00}{?} \} ) \) in Koordinatenform an.
Bemerkung: Das '\(\{ \colorbox{#ffff00}{?} \}\)' steht für