Aufgabe:Aufgabe:b)Versuche eine Regel zur Bestimmung von Ereigniswahrscheinlichkeiten zu finden wenn Bedinung für Simons Regel nicht erfüllt sind .....Simons Regeln:Um die Wahrscheinlichkeit p eines Ereignisses E zu berechnen kann die Zahl der Ergebnisse die zu E gehören durch die Zahl aller möglichen Ergebnisse teilen..........Bei a musst man Erklären warum Simons Regel nur bedingt stimmt und welche Voraussetzung man brauch dami es klappt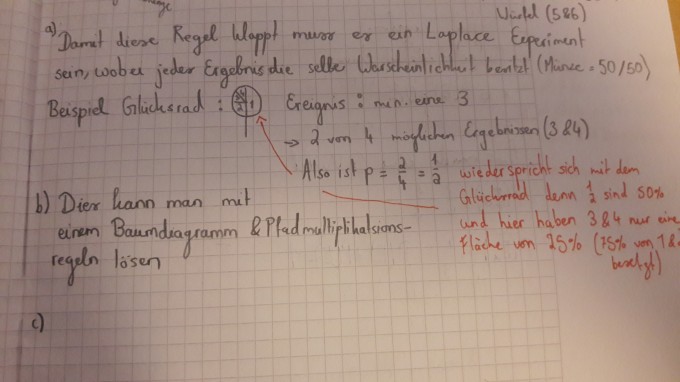 Simons
Simons
Problem/Ansatz:Hallo ich brauche Hilfe bei der Aufgabe b, ich hab sehr lange nachgedacht jedoch finde ich keine Regel.....Die Aufgabe a hab ich bearbeitet vlt hilft diese zur Lösung des Problems(Bilder)......Lg Danke