Vom Duplikat:
Titel: (i) Bestimmen Sie den linearen Term im charakteristischen Polynom χA(T) = det(T E − A) der allgemeinen 3 × 3-Matrix
Stichworte: eigenwerte,diagonalisierbar,matrix,charakteristisches-polynom
(i) Bestimmen Sie den linearen Term im charakteristischen Polynom χA(T) = det(T E − A) der allgemeinen 3 × 3-Matrix
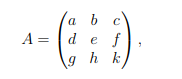
vermöge der Jägerzaunregel.
(ii) Berechnen Sie die Determinante der 4 × 4-Matrix
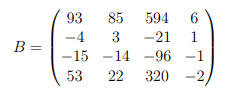
durch geschickte Zeilen- und Spaltenoperationen. (Hinweis: Das Ergebnis ist
eine einstellige Zahl.)