Hallo MontanaCore,
hier die versprochenen Berechnungen:
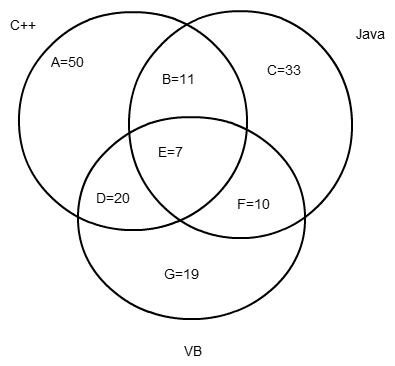
Den gegebenen Angaben und dem Diagramm können wir entnehmen
A = 50
C = 33
G = 19
B + D + E + F = 48
B + D + F = 41
Also E = 48 - 41 = 7
A + B + D + E = 88 | A = 50, E = 7
B + D = 88 - 57 = 31
B + D + E + F
31 + 7 + F = 48
Also
F = 48 - 38 = 10
Ich denke jetzt, dass es doch heißen muss
B + E = 18
B + 7 = 18
B = 11
Und da
B + D = 31
D = 31 - 11 = 20
Wir haben jetzt
A = 50
B = 11
C = 33
D = 20
E = 7
F = 10
G = 19
Die Summe 150 stimmt schon mal :-)
Zeichnen wir alles nochmal in ein Diagramm ein:
Ich kann momentan keine Fehler entdecken :-D
Anzahl der Bewerber, die alle 3 Programmiersprachen können: E = 7
Anzahl der Bewerber, die nicht C++ können, aber Java und VB (beides?) beherrschen: F = 10
Anzahl der Bewerber, die VB und C++ beherrschen: D + E = 27
Besten Gruß