Substitution alles substituieren?

Question

Aufgabe:

Problem/Ansatz:

ich habe eine generelle Frage zur Substitution. Wenn man jetzt beispielsweise x^2 durch u ersetzt, ersetzt man dann alle vorhandenen x im Integral durch u? Ich hab das jetzt mehrmals unterschiedlich gesehen, bin deshalb verwirrt. Beim folgenden integral substituiert man beispielsweise nicht alle x:

∫(e^x^(1/2))/x^(1/2)dx = ∫(e^u)/x^(1/2) * 2x^(1/2)du = 2e^x^(1/2)

Aber bei diesem Integral wurden beispielsweise alle x substituiert:

∫x^3*(1+x^2)^(1/2) = 1/2* ∫ (u^(3/2)-u^(1/2)) du

Wie geht man also vor?

Answer 1

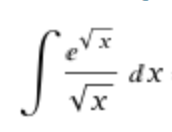
Bei dem 1. Integral substituierst Du:

z=√x

----------------------------------------------------

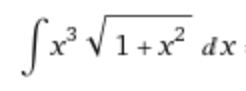
Bei dem 2. Integral kannst Du substituieren:

z= x^2 oder

z=1+x^2

Du kannst nicht sagen, weil das bei dem einen Integral so ist , muß das bei dem anderen Integral so sein.

Integrieren ist eine Sache der Übung.

Kleiner Tipp:

Meistend führt eine Substitution der kompletten Wurzel oder was komplett in der Wurzel steht, zum Erfolg.

Das muß jedoch machmal probieren.

Comments

ok, aber muss man also nicht jedesmal jedes x substituieren?

---

Du mußt das so machen, das nach der Substitution alles dann mit z steht (wenn mit z substituiert wird)

Wenn noch was mit x steht , mußt Du das als z ausdrücken.

---

Danke, aber bei dem ersten Integral wird doch Wurzel x im Nenner nicht Substituiert, weil man es sonst ja nicht Wegkürzen kann

---

wenn die Aufgabe so lautet , dann wird der Nenner auch substituiert.