Funktion einer ganzrationalen Funktion vierten Grades bestimmen?

Question

Aufgabe:

Ich bräuchte Hilfe bei der folgenden Aufgabe:

Bestimmen Sie die Funktionsgleichung einer geraden, ganzrationalen Funktion 4. Grades, deren Graph symmetrisch zur y-Achse ist und durch A (-4|0), B(4|0) und C (0|4) verläuft.

Problem/Ansatz:

Ich habe bereits die allgemeine Funktionsgleichung aufgestellt und dabei die ungeraden Exponenten bereits weg gelassen.

f(x)=ax⁴+bx²+c

Wie mache ich denn jetzt weiter??

Answer 1

Bestimmen Sie die Funktionsgleichung einer geraden, ganzrationalen Funktion 4. Grades, deren Graph symmetrisch zur y-Achse ist und durch A (-4|0), B(4|0) und C (0|4) verläuft.

Ungünstiger Ansatz

f(x) = a·x^4 + b·x^2 + c

f(4) = 0 --> a·4^4 + b·4^2 + 4 = 0 --> b = - 16·a - 1/4

f(0) = 4 → c = 4

f(x) = a·x^4 - (16·a + 1/4)·x^2 + 4

Leichter Ansatz

f(x) = a·(x^2 - 16)·(x^2 - n)

f(0) = a·(-16)·(-n) = 4 --> a = 1/(4·n)

f(x) = 1/(4·n)·(x^2 - 16)·(x^2 - n)

Für n könnte man jetzt jeden beliebigen wert einsetzen.

Answer 2

Bei "irgendwie durch die 3 Punkte", kann man die Formel von  Der_Mathecoach

verwenden. das variable n habe ich mal per aB[0] variiert: http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm

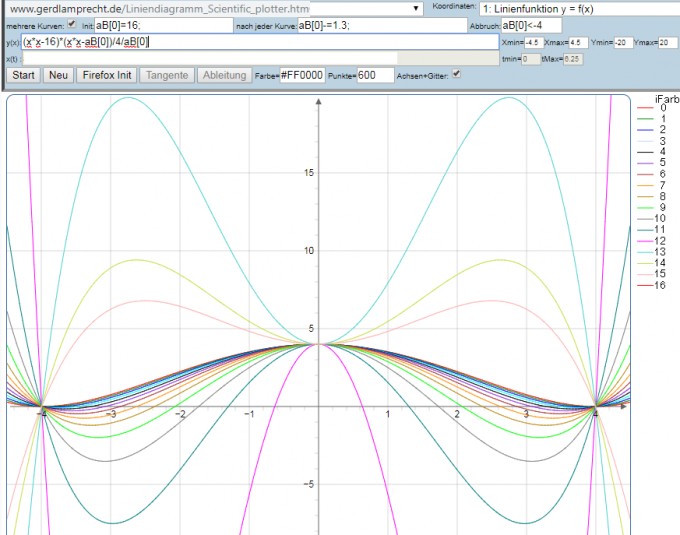
Bei "nur die beiden sym. Nullstellen A, B" kann man es sich einfacher machen:

- einfache Parabel dafür lautet 4-x²/4

Damit der Graph jedoch nicht negativ wird und weitere Nullstellen erzeugt, einfach quadrieren: (4-x²/4)²

und Maximum anpassen mit Wurzel(4)=2 wird es zu (2-x²/4)² und durch Halbierung des Offset auch x² halbieren:

 f(x)=(2-x²/8)² = x^4/64 - x^2/2 + 4

was Spezialfall n=aB[0]=16 entspricht.

(x*x-16)*(x*x-16)/4/16 = x^4/64 - x^2/2 + 4