Bestimme die Gleichung einer ganzrationalen Funktion vierten Grades, die den Verlauf der Umgehungsstraße …

Question

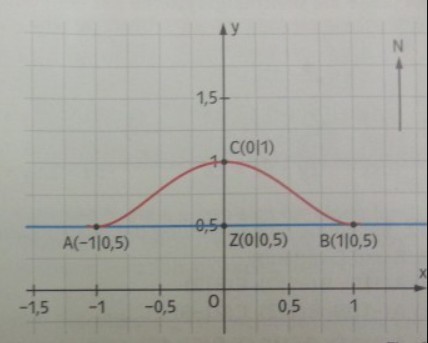
Durch das Zentrum \( Z \) eines Dorfes führt eine geradlinige Hauptstraße. Es soll eine Umgehungsstraße gebaut werden, die symmetrisch zur Nord-Süd-Achse des Dorfes verläuft, in \( A \) und \( B \) tangential in de geradlinige Hauptstraße mündet und \( 500 \mathrm{~m} \) nördlich vom Dorfzentrum durch den Punkt \( C \) führt (vgl. Abbildung, eine LE entspricht \( 1 \mathrm{~km} \) ).

Bestimme die Gleichung einer ganzrationalen Funktion vierten Grades, die den Verlauf der Umgehungsstraße für \( -1 \leqq x \leqq 1 \) beschreiben könnte.

Ansatz:

f(0)=1 ; f´(0)=0 ; f(-1)=0,5 ; f(1)=0,5 und die 5. Bedienung ?, ich weiß, dass die ungeraden Exponenten wegfallen.   ax⁴+bx²+e=f(x)     e=1    so  es bleiben  ax⁴+bx²+1=f(x)

f(1)=a+c+1=0,5      a=0.5-c
f(-1)=0,5-c+c+1=0,5      -c+c=-1  ?

Answer 1

Allgemein wird korrekterweise für knickfreie Splines dieser Ansatz verwendet:
$$ f(x)= ax^5+bx^4+cx^3+dx^2+ex+f $$
Bedingungen:
Stelle x=-1:
$$f(-1)=0,5$$
$$f'(-1)=0$$
$$f''(-1)=0$$
Stelle x=0:
$$f(0)=1$$
$$f'(0)=0$$
Stelle x=1:
$$f(1)=0,5$$
$$f'(1)=0$$
$$f''(1)=0$$
$$ f'(x)= 5ax^4+4bx^3+3cx^2+2dx+e $$
$$ f''(x)= 20ax^3+12bx^2+6cx+2d $$
Bedingungen einsetzen, Gleichungssystem erstellen, lösen ist ein wenig Fleiss, aber bei den Werten fliegt wohl ziemlich viel in die Tonne.

Comments

ja danke sehr, ich habe dann erkannt das die Punkte A und B auch Tiefpunkte sind, und hatte dann genug bedienungen für den Gtr 

Answer 2

Auch wenn ich persönlich die Löung von Moliets schön finde entspricht sie nicht dem Unterricht der 11. Klasse von Steckbriefaufgaben.

Wir wählen den Ansatz einer Funktion 4. Grades mit den Bedingungen

f(x) = ax^4 + bx^3 + cx^2 + dx + e

d = b = 0
f(0) = 1
f(1) = 0.5
f'(1) = 0

Daraus folgt das Gleichungssystem

d = b = 0
e = 1
a + b + c + d + e = 1/2
4·a + 3·b + 2·c + d = 0

und die folgende Lösung der Funktionsgleichung

f(x) = 0,5·x^4 - x^2 + 1

Answer 3

Ich verschiebe den Graph um \( 0,5\) Einheiten nach unten:

\(A´(-1|0)\) und \(B´(1|0)\)   Hier sind jeweils doppelte Nullstellen:

\( f(x)=a(x+1)^2(x-1)^2\)

\(C´(0|0,5)\):

\( f(0)=a(0+1)^2(0-1)^2=a\)

\(a=0,5\)

\( f(x)=0,5(x+1)^2(x-1)^2\)

nach oben:

\( p(x)=0,5(x+1)^2(x-1)^2+0,5\)