Rechteck in Kreis maximieren? Stimmt der Ansatz?

Question

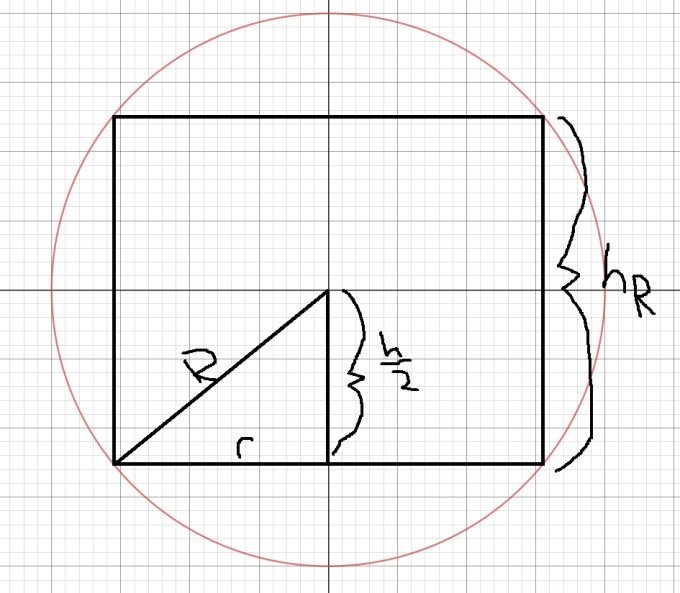
Extremalbedingung:$$A(r,h_R)=2r\cdot h_R$$ Nebenbedingung:$$h_R^2+(2r)^2=(2R)^2 \quad \Longrightarrow h_R=\sqrt{(2R)^2-(2r)^2}$$ Zielfunktion:$$A_R(r)=2r\cdot \sqrt{(2R)^2-(2r)^2}$$  Stimmt dieser Ansatz? Und ist das nicht eine Aufgabe, die man mit dem Lagrangschen Optimierungsverfahren effizienter lösen kann?

Answer 1

Der Ansatz stimmt, wie es von dir zu erwarten war.  Aber das willst du gar nicht wissen. Zum Lagrangschen Optimierungsverfahren weiß ich leider nichts.