Hallo Polly,
Jetzt muss ich berechnen ob sie kollinear sind aber ohne t zu kennen.
Ich verstehe die Aufgabe so, dass man \(t\) so berechnen soll, so dass \(\vec{AB} = k \cdot \vec{AC_t} \) ist (s. Kollinearität)
Stelle die Vektoren \(\vec{AB}\) und \(\vec{AC_t}\) auf: $$\vec{AB} = B-A = \begin{pmatrix} 4\\ 5\\ 9\end{pmatrix} - \begin{pmatrix} 1\\ 1\\ 1\end{pmatrix} = \begin{pmatrix} 3\\ 4\\ 8\end{pmatrix}\\ \vec{AC_t} = C_t - A = \begin{pmatrix} 1\\ t \\ 5 \end{pmatrix} - \begin{pmatrix} 1\\ 1\\ 1\end{pmatrix} = \begin{pmatrix} 0\\ t-1\\ 4\end{pmatrix} $$'kollinear' bedeutet, dass sich der eine Vektor durch Multiplikation mit einem Skalar in den anderen überführen lässt (s.o.). Das ist hier nicht möglich, da die Kombination der \(x\) und \(z\) Koordinate bereits in verschiedene Richtungen zeigen, aber gar nicht von \(t\) abhängig sind, also konstant sind.
Auch die drei Punkte \(A\) \(B\) und \(C_t\) können nicht kollinear sein (also auf einer Geraden liegen), da sich die Gerade durch \(A\) und \(B\) (rot) sich nicht mit \(C_t\) (grün) schneidet $$C_t: \quad \vec{x} = \begin{pmatrix} 1\\ 0 \\ 5 \end{pmatrix} + t \cdot \begin{pmatrix} 0\\ 1 \\ 0 \end{pmatrix}$$
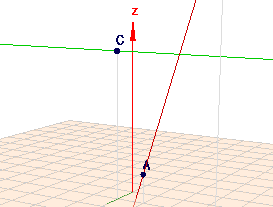
(klick auf das Bild)
Die Lösungsmenge für Deine Aufgabe ist also leer!
Gruß Werner