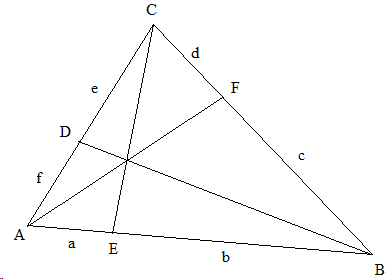
Der Satz von Ceva besagt: Wenn auf den Seiten eines Dreiecks ABC die Punkte D, E und F liegen, welche die Seiten in den Verhältnissen a/b, c/d und e/f teilen und die Strecken von je einem Eckpunkt des Dreiecks zum gegenüberliegenden Teilungspunkt durch einen gemeinsamen Punkt gehen, dann ist das Produkt der Teilungsverhältnisse gleich 1 (f/e∙b/a∙d/c=1). Wie beweist man das?