Problem bei Berechnung einer linearen Funktion mit einer Wurzel

Question

1.   2x+\( \sqrt{\frac{4}{9}} \)  = 1 | - \( \sqrt{\frac{4}{9}} \)

2.   2x = \( \frac{1}{3} \) | :2

3.   x = \( \frac{1}{6} \)

So wird die Gleichung berechnet, aber \( \sqrt{\frac{4}{9}} \) kann doch auch ( - \( \frac{2}{3} \) ) sein, da es für eine Wurzel ja zwei Lösungen geben kann. Plus und Minus. Somit müsste es doch theoretisch zwei Lösungen geben. Wenn das gegen eine mathematische Regel ist, könntet ihr mir diese auch erklären?

Comments

da es für eine Wurzel ja zwei Lösungen geben kann.

Wer hat dir den Unfug erzählt?

"Lösungen der Gleichung x²=a" ist im Reellen  NICHT das Gleiche wie "Wurzel aus a"

---

ja das weiß ich auch, aber könntest du mir genau erklären warum das nicht das gleiche ist. weil im prinzip ist minus zwei mal minus zwei auch vier

---

Aber hier hat keine Zahl eine gerade Potenz.

---

ja das weiß ich auch, aber könntest du mir genau erklären warum das nicht das gleiche ist. weil im prinzip ist minus zwei mal minus zwei auch vier

Dann zieh dir doch mal die Definition der Quadratwurzel rein:

https://de.wikipedia.org/wiki/Quadratwurzel

Answer 1

dein Rechenweg ist korrekt.

Das mit den zwei Ergebnissen der Wurzel verwechselst du glaube ich.

Angenommen, du hast die Gleichung x²=4, also irgendeine Zahl x mit sich selbst multipliziert ergibt vier. Dann gibt es für den Wert von x zwei Möglichkeiten (2 und -2), da bei der Multiplikation mit zwei negativen Vorzeichen, sich dieses umdreht. 2*2 = 4 und (-2)*(-2)=4. Haben wir aber, wie in deinem Beispiel keine quadrierte Zahl, sondern lediglich eine Wurzel, dann beschränken wir uns auf das nicht negative Ergebnis, da die Wurzelfunktion für negative Zahlen nicht definiert ist.

Comments

wenn man von 4²  die wurzel zieht gibt das doch 4

---

Ja, das tut es.

Ist vielleicht etwas schwammig formuliert. Ich ändere es nochmal.

---

wenn man von 4²  die wurzel zieht gibt das doch 4

Das ist für das Problem relativ unerheblich.

Wenn man von (-4)² die Wurzel zieht, ergibt das auch 4.

---

jetzt verstehe ich das überhaupt nicht mehr

---

warum ist das mal so mal so, und warum wird das jetzt zur 4

---

(-4)*(-4)=16 → √16 = 4

---

warum kann das aber nicht -4 sein? ergibt doch auch 16

---

Deine Frage zeigt mir, dass du die Definition NICHT gelesen hast.

Wenn jemand das Wort "Bank" sagt, denkt einer an eine Sitzgelegenheit, der andere an ein Kreditinstitut.

Um solche Missverständnisse zu vermeiden, gibt ers in der Mathematik klare DEFINITIONEN.

Und wenn du weiterhin mit anderen ;Mathematikern über "Wurzeln" sprechen willst, dann lerne endlich (heißt: lies vorher die Definition) was der Begriff (Quadrat)Wurzel in der Mathematik bedeutet.

---

Die Wurzel einer Zahl x ist immer positiv. Es ist eine Konvention.

Denn, betrachten wir das Radizieren als eine math. Funktion, so existiert für den Wert x, den ich in die Funktion einsetze, genau ein Wert als Ergebnis. Würde man beide Werte nehmen, so wäre die Quadratwurzel nicht mehr eindeutig.

---

Die Wurzel einer Zahl x ist immer positiv. Es ist eine Konvention.

Jetzt musst du aber auch die Definition lesen, denn deine Aussage ist so ebenfalls unkorrekt.

---

Natürlich habe ich das gelesen, trotzdem verstehe ich nicht, warum das so ist

---

Es ist so festgelegt (wenn dir das Wort "definiert" nicht eindringlich genug ist).

---

Hat also keinen schönen mathematischen Sinn dahinter? :D

---

Ich weiß ja nicht, was für dich "schön" ist. Dafür gibt es keine mathematische Definition, deshalb kann jeder Einzelne etwas anderes als schön empfinden.

Der Sinn ist vermutlich, dass man den Begriff der Wurzel eindeutig (und nicht mehrdeutig) interpretieren wollte.

Larry scheint inzwischen schlafen gegangen zu sein. Kleine Übung für dich zum Verständnis der Definition: Warum war seine Aussage falsch?

---

Ich verstehe dich RainMan. Aber akzeptiere es einfach für den Moment. Entweder du wirst es brauchen oder nicht, aber lernen musst du es trotzdem für dein Ziel oder für deine Schule, egal ob es für dich unlogisch ist oder logisch. Es gibt viele Sachen in der Mathematik, bei denen man sagen könnte: Da hat ja einfach ein kluges Hirn gesagt, dass das so ist und es geht so auf und jetzt müssen es alle befolgen. Natürlich ist das eine naive Denkhaltung, die du dir mit der Zeit selber aus dem Kopf schaffen wirst. Eine Definition in der Mathematik muss nicht unbedingt mit allen Situationen übereinstimmen. Es kommt einfach darauf an, ob es nützlich ist oder nicht. Wir machen Mathematik nicht, um uns zu quälen, sondern die ganzen neuen Sachen die erfunden werden, die benötigen eben genau solche Definitionen und Sachen, auch wenn es vielleicht unlogisch oder nicht nachvollziehbar erscheint. Es klappt ja und das ist das wichtigste.

---

Und bei Funktionen zweiten Grades hat die Wurzel dann wieder zwei Lösungen?

---

Eine Definition in der Mathematik muss nicht unbedingt mit allen Situationen übereinstimmen.

Sie sollte schon in allen Situationen Bestand haben.

Auch die Einschränkung "Wurzel aus 16 ist nur 4 und nicht auch noch -4" erlaubt ja trotzdem, BEIDE Lösungen der Gleichung x²=16 anzugeben.

Die eine Lösung ist x=√16 (also x=4), und die zweite Lösung ist 
x=-√16 (also x=-4).

---

Larry scheint inzwischen schlafen gegangen zu sein.

Noch nicht ganz.

Stört dich das "positiv" wegen der somit ausgeschlossenen 0? Oder sollte ich es lieber formulieren als "Das Ergebnis des Radizierens einer Zahl x ist meistens eine positive reelle Zahl"?

Oder der Begriff "Konvention"? Man könnte es auch so formulieren, dass die Wurzel'funktion' bei Annahme der beider Werte eher eine Wurzel'relation' ist.

---

Eine quadratische Funktion "zweiten Grades" kann MAXIMAL zwei Lösungen haben, aber es muss nicht immer so sein. Eine Polynomfunktion "dritten Grades" kann MAXIMAL 3 Lösungen haben, aber es muss nicht immer so sein. Es kommt immer auf die Graphsituation drauf an.

Bei der quadratischen Funktion entscheidet die Diskriminate, also der Term unter der Wurzel bei der PQ oder abc Formel über die Lösungen. Wenn du eine positive Zahl unter der Wurzel hast, dann hast du 2 Lösungen. Wenn die Diskriminate 0 ist, dann hast du eine Lösung. Wenn die Diskriminate negativ ist, dann hast du zumindest in der Schulmathematik keine Lösung, da die Wurzel dadurch undefiniert wird.

---

Und bei Funktionen zweiten Grades hat die Wurzel dann wieder zwei Lösungen?

Nein. Die GLEICHUNG hat eventuell zwei Lösungen, aber wenn du aus eine konkreten Zahl eine Wurzel ziehst, kann es maximal eine Wurzel geben.

Hast du inzwischen das Larry-Problem lösen können.

---

abakus, lass ihn einfach überlegen. Er wird schon darüber hinweg kommen und es glauben.

---

Mit dem Larry Problem meinst du wohl weil er gesagt hat dass es keine negativen wurzeln gibt. Die Wurzel muss ja nur innen positiv sein sonst hat sie keine lösung

---

Stört dich das "positiv" wegen der somit ausgeschlossenen 0? Oder sollte ich es lieber formulieren als "Das Ergebnis des Radizierens einer Zahl x ist meistens eine positive reelle Zahl"?

Ja, da liegt dein Fehler. Dein Alternativvorschlag zeigt aber, dass du die Definition immer noch nicht richtig gelesen hast, sonst würdest du nicht so ein Verlegenheitsgesülze wie  "meistens eine positive reelle Zahl" bringen.

Wie soll ich Rainman von der Notwendigkeit von Definitionen überzeugen, wenn selbst ein gestandenes Mitglied wie du  das nicht ernsthaft verfolgt.

---

Atorian ich glaub es ja und ich akzeptiere es auch, aber ich würde es gerne auch verstehen. Vor allem weil die Wurzel ja in der Gleichung vorkam. Wenn die 1 und die 2 oben nicht wäre dann weiß ich jetzt nicht ob es doch zwei lösungen geben würde

---

Wenn ich jetzt die Gleichung habe x = \( \sqrt{\frac{4}{9}} \) hat die gleichung dann zwei lösungen?

---

Nein. Die Wurzel aus 4/9 ist 2/3 und nichts anderes.

Etwas anderes ist die Gleichung x²=4/9. Die hat die beiden Lösungen

√(4/9)  , also 2/3, und 

-√(4/9)  , also -(2/3).

---

Und wenn ich bei meiner Gleichung oben statt 2x 2x²  haben würde und ich würde wurzel 4/9 rüber zur eins bringen, hat das nicht dann zwei Lösungen?

---

verstehst du was ich meine?

---

Die Gleichung 2x²=1/3 hätte zwei Lösungen: √(1(6) und -√(1(6).

---

Verlegenheitsgesülze wie  "meistens eine positive reelle Zahl" bringen.

Um aus dem W.-Artikel zu zitieren: "Hierbei ist [...] \(a\) [...] häufig eine nichtnegative reelle Zahl"

---

ja okay, dann hat sich zumindest mein Problem beim rechnen geklärt

---

GENAU DARUM ging es mir. In der Definition steht, dass die Wurzel eine nichtnegative Zahl ist. Das ist was anderes als "positive Zahl".

Was soll da dein "meistens positiv"? Das könnte ja auch bedeutet "in seltenen Ausnahmefällen auch mal negativ".

---

Ich verstehe dein Problem nicht. Eine normale Wurzel zu ziehen ist doch nicht schlimm.

Wenn du zum Beispiel diese quadratische Gleichung lösen willst:

x^2+3 = 10 Wie gehst du dann vor?

x^2 = 7

x = + - Wurzel aus 7

Du kannst eine Gleichung immer als Funktion oder Gerade aufzeichnen. Um den gemeinsamen Wert zu finden, versucht man ja eben die Gleichung so umzustellen, dass man die Punkte findet, die sich schneiden.

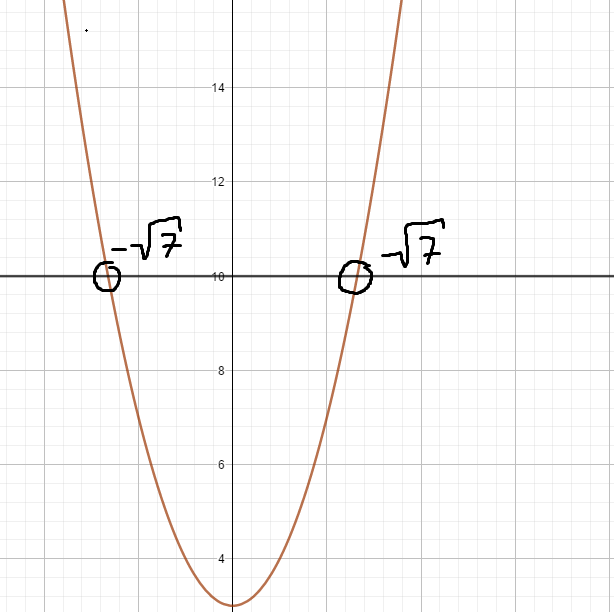
Ich zeige es dir anhand eines Graphens. Siehst du. Hier gibt es zwei Schnittpunkte. Du hättest also mit der positiven Wurzel aus 7 nur den einten Schnittpunkt und den anderen verloren. Deshalb muss man das machen. x^2 ist eine Parabel und die andere Seite eine Gerade... Parabel und Gerade schneiden sich in diesem Fall genau so, dass es zwei Lösungen gibt.

---

Jetzt hab ichs.

Also, das Ergebnis des Radizierens ist eine positive reelle Zahl oder null.

---

"Hierbei ist [...] a [...] häufig eine nichtnegative reelle Zahl"

Kannst du einen Screenshot dieser Zeife liefern? Dies Suchfunktion mit

"eine nichtnegative reelle Zahl" liefert auf dieser Seite keinen Treffer.

---

Fast ganz oben.

---

RainMan so sieht deine Gleichung aus. Verstehst du das jetzt? Du hast keine Parabel in der Gleichung, weil dort kein x^2 vorkommt oder sonst was, sondern du hast dort einen schönen Term, bei dem sogar Quadratzahlen stehen, die du schön mit der Wurzel ziehen kannst.  Bei dir gibt es zwei Geraden. Das wirst du auf der Grafik sehen.

---

Ich hoffe, dass du jetzt den Unterschied zwischen Wurzelziehen Wurzel aus 4 und Wurzel aus einem x^2 ziehen in einer Gleichung verstehst.

---

Ja alles klar jetzt, danke

---

Bitte. Falls du noch Fragen hast, dann frag mich ruhig. Ich bin natürlich auch nur ein Schüler und erzähle dir nur das, was ein Schüler halt so weiss.

Answer 2

Wie Abakus schon ausgeführt hat ist √(4/9)=2/3.

Comments

ja das habe ich auch schon so ausgeführt oben