f(x) = -x^3 + 3·x^2 - 2·x
f(1) = 0 → W(1 | 0)
g(x) = m·(x - 1) = m·x - m
-x^3 + 3·x^2 - 2·x = m·x - m
-x^3 + 3·x^2 - 2·x = m·x - m
x^3 - 3·x^2 + m·x + 2·x - m = 0 → Eine Nullstelle ist garantiert der Schnittpunkt x = 1
(x^3 - 3·x^2 + m·x + 2·x - m) / (x - 1) = x^2 - 2·x + m
x^2 - 2·x + m = 0 --> x = 1 ± √(1 - m)
Wann gibt es hier keine Lösung → m > 1
Genau eine Lösung → m = 1
Genau 2 Lösungen → m < 1
Für das jeweilige m gibt es also vieviele Lösungen
m > 1 → nur einen Schnittpunkt
m = 1 → einen Schnittpunkt der Berührpunkt ist
m < 1 → drei Schnittpunkte
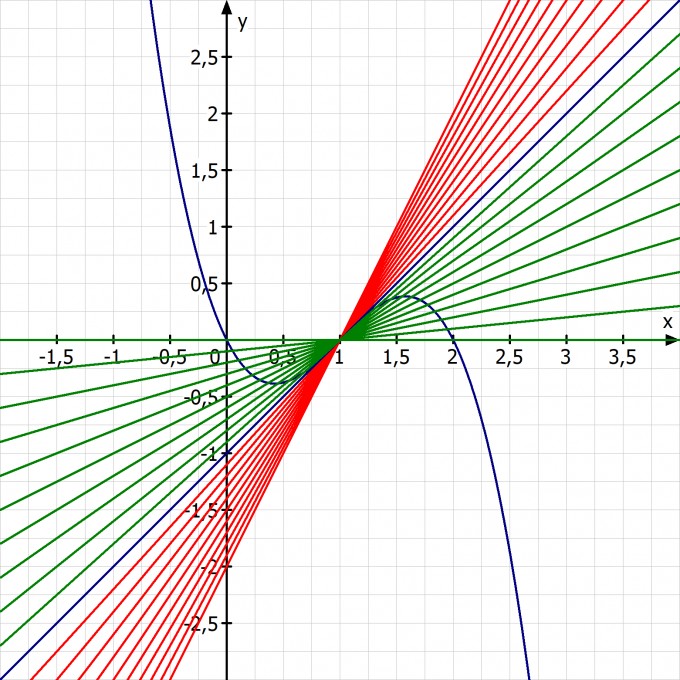
Hier eine Skizze