Gesamtkostenfunktion , Gewinnfunktion mithilfe variable Stückkosten und Preis-absatz funktion berechnen

Question

Aufgabe:

Folgende Daten sind vorhanden:

variable Stückkosten:    kvar(x) = − 1/3 x^2 + 5x + 200
Fixkosten:                          fix= 600
Preis-Absatz-Funktion: p(x) = 400 −10x

1. Ermitteln Sie die (Gesamt-)Kostenfunktion!
2. Wie lautet die Gewinnfunktion?
3. Wie viel Stück seines Produktes muss der Monopolist absetzen, um den
maximalen Gewinn zu erzielen.
4. Wie hoch ist in diesem Fall sein Gewinn?

Problem/Ansatz:

1. 17x x^2+5x+200 | * x

K(x) = 1/3x^3 + 5x^2+200x + 600

2. p(x)= 400 - 10x | * x

G(x)= E(x) - K(x)

G(x) = 400x-10x^2- ( 1/3x^3 + 200x - 15x^2 - 600)

=  1/3x^3 -15x^2+200x-600

3. Hier habe ich die mir die Lösung aufgeschrieben

G'(x)= 2/3x - 30x + 200

29,34x = 200

x= 6,81

Kann leider die erste Ableitung nicht mehr nachvollziehen, es müsste doch eigentlich heißen:

= 2/3x^2 + 200 -30x   ???

Und dann mithilfe der pq formel ausrechnen??

4. Und dann müsste ich ja die 6.81 in G(x) einfügen, als Ergebnis habe ich mir Aufgeschrieben = 81,82

Voraussgesetzt die Gewinn funktion stimmt, komme ich jedoch auf 171.63

Comments

Oder muss ich für die Nr 3 nicht die Erlösfunktion und die Kostenfunktion ableiten und gleichsetzten und nach x auflösen??

Dann wäre aber mein Problem, das ich x^2 und x stehen habe und nicht auflösen kann :(

400-20x = 2/3x^2+200-30x

---

Zur Aufgabe 3 nun meine neue Lösung . Wäre sehr dankbar wenn mir das jemand Bestätigen könnte..

G'(x) = x^2 -30x -200

pq-formel:

-30/2 +- √(-30/2)^2 + 200

-15 +- 20,6

x1= 5,6 (Abzusetzte Menge)

x2= -35,6

Zur Aufgabe 4)

G(5,6) = 1/3(5,6)^3 -15(5,6)^2 + 200(5,6) -600

= 108,53

---

Ich sehe gerade da haben sich ein paar Fehler eingeschlichen....  die 17x vor 1. sollten da natürlich nicht hin.. und die Kostenfunktion sollte natürlich ein minus Zeichen davor haben.

---

Allerdings, da sind ein paar Fehler. Willst du es nochmal aufschreiben ohne Fehler? Deine Ansätze sehen insgesamt ganz gut aus. Aber du machst eine Menge Flüchtigkeitsfehler beim ausrechnen.

---

So, ich habe alle erkannten Fehler korrigiert. Hier nochmal die Aufgabenstellung und meine Lösungen dazu. Wäre wirklich SEHR dankbar, wenn mir jemand die Ergebnisse bestätigen könnte. Bin mir bei der Nummer 3 unsicher, vor allem nach dem ich meine Fehler korrigiert habe

 :(

Liebe Grüße & Vielen Dank!

Aufgabenstellung:

variable Stückkosten:    kvar(x) = − 1/3 x^2 + 5x + 200
Fixkosten: 600
Preis-Absatz-Funktion: p(x) = 400 −10x

1. Ermitteln Sie die (Gesamt-)Kostenfunktion!
2. Wie lautet die Gewinnfunktion?
3. Wie viel Stück seines Produktes muss der Monopolist absetzen, um den
maximalen Gewinn zu erzielen.
4. Wie hoch ist in diesem Fall sein Gewinn?


Meine Lösungen
Aufgabe 1.)

− 1/3 x^2 + 5x + 200 | * x

K(x) = -1/3x^3 + 5x^2+200x + 600



Aufgabe 2.)

p(x)= 400 - 10x | * x

G(x)= E(x) - K(x)

G(x) = 400x-10x^2- (-1/3x^3 + 5x^2+200x + 600 )

=  1/3x^3 -15x^2+200x-600

Aufgabe 3.)

G'(x) = x^2 -30x + 200

pq-formel:
Da ich annehme das keine negativen Ergebnisse rauskommen können, habe ich das Minus Zeichen vor der eigentlichen pq-Formel weggelassen

30/2 +- √(-30/2)^2 - 200

15 +- 5

x1= 20

x2= 10

Aufgabe 4.)

Jetzt da ich die Fehler korrigiert habe und ich zwei positive Zahlen raus bekomme, weiß ich leider nicht welche die Menge darstellen soll. An sich würde Ich aber die errechnete Menge in G(x) "stecken" um den Gewinn auszurechnen

Answer 1

Hallo Tommy,

habe deine - inzwischen ziemlich richtigen Ausführungen - in deinem letzten Kommentar erst nach meiner Antwort gesehen. Trotzdem kannst du ihr noch Nützliches entnehmen.

1. Ermitteln Sie die (Gesamt-)Kostenfunktion!

Hier hast du das Minuszeichen vor -1/3 vergessen:

K(x) = - 1/3·x^3 + 5·x^2 + 200·x + 600

Der Definitionsbereich von K(x) sollte eigenlich auf D_ÖK = [0 , 20]  beschränkt sein, weil ab x=20 die Werte wieder abnehmen!

2. Wie lautet die Gewinnfunktion?

E(x) - K(x) = p(x) * x - K(x)

G(x) = (400 - 10·x)·x - (- 1/3·x^3 + 5·x^2 + 200·x + 600)  =  1/3 · x^3 - 15·x^2 + 200·x - 600

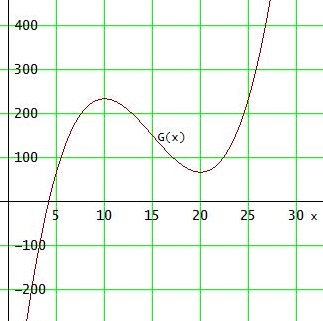
3. Wie viel Stück seines Produktes muss der Monopolist absetzen, um den
maximalen Gewinn zu erzielen.

G '(x) = x^2 - 30·x + 200    (hast du richtig)

x^2 - 30·x + 200 = 0    bei deiner pq-Formel muss vorn  - p/2 = 30/2 = 15 stehen.

das ergibt dann  ein lokales Maximum bei  x=10   (G "(10) < 0 ! ,  Minimum bei x=20)

Wenn jetzt im Text eine maximale Produktionsmenge x_max ( die kann ja nicht unendlich sein!) gegeben wäre (?), müsste man  G(10)  mit  G(x_max)  vergleichen  und der x-Wert mit dem größeren Gewinn wäre die Menge mit dem absoluten Gewinnmaximum. (Vgl. die Bemerkung zur Kostenfunktion)

4. Wie hoch ist in diesem Fall sein Gewinn?

Wenn man davon ausgeht, dass bei  x = 10 das absolute Gewinnmaximum vorliegt, wäre dieser:

G(10)  =  700/3  ≈  233,33  

Gruß Wolfgang

Comments

Tatsächlich ist das eine abgewandelte Version der Aufgabe in der die max. Produktionsmenge nicht gegeben war.

Noch eine Frage, sie haben bei der Gewinnfunktion -9x^2 da stehen.
Das müsste aber doch -15x^2 heißen??

Sonst wäre ja auch meine Ableitung falsch, ich nehme an , Sie haben sich da vertippt.

Trotzdem ein dickes Dankeschön an sie, sie haben mir in den letzten Tagen wirklich super Geholfen !!

---

Du hast recht, habe mich da leider vertippt. Ist  Alle Rechnungen wurden aber  mit

G(x) = 1/3 · x³ - 15·x² + 200·x - 600  durchgeführt.

Habe das in der Antwort korrigiert.