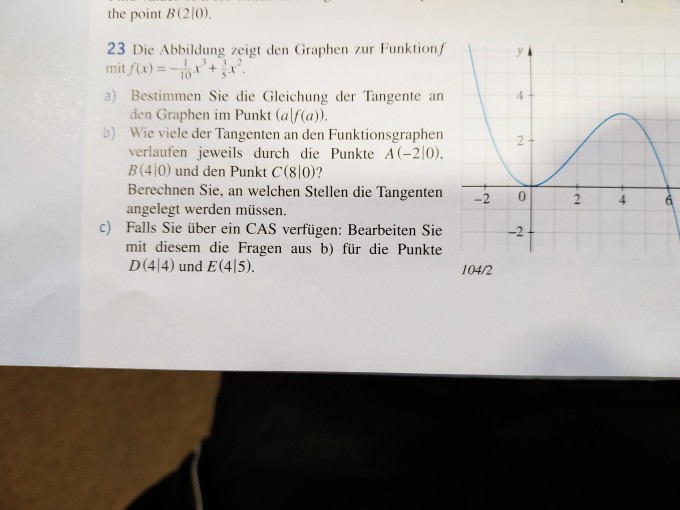
Die Abbildung zeigt den Graphen zur Funktion f mit f(x) = -1/10·x^3 + 3/5·x^2.
a) Bestimmen Sie die Gleichung der Tangente an den Graphen im Punkt (a | f(a)).
b) Wie viele der Tangenten an den Funktionsgraphen jeweils durch die Punkte A(-2 | 0), B(4 | 0) und C(8 | 0)? Berechnen Sie, an welchen Stellen die Tangenten angelegt werden müssen.
c) Falls Sie über ein CAS verfügen: Bearbeiten Sie mit diesem die Fragen aus b) für die Punkte D(4 | 4) und E(4 | 5).