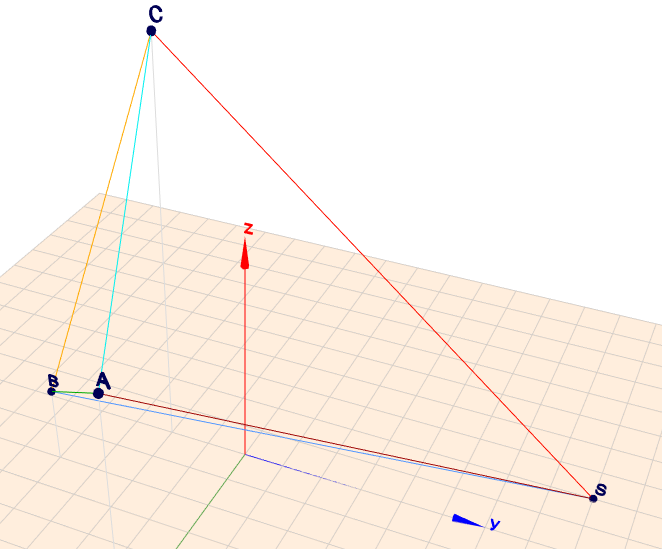
1)
Berechne \(F=\frac{1}{2}\left|\overrightarrow{AB}\times\overrightarrow{AC}\right|\). Das Kreuzprodukt von \(\overrightarrow{AB}\) und \(\overrightarrow{AC}\) ist \(\begin{pmatrix} -24\\40\\-16 \end{pmatrix}\)
2)
Das Volumen eines Tetraeders, ist ähnlich der Volumenformel einer Pyramide. Nur halt mit Skalierungsfaktor, weil es anstatt von einem Paralellogramm ein Dreieck besitzt. Ich bevorzuge es, mit der Determinante zu rechnen. Beide Rechenwege sind möglich:$$V=\frac{1}{6}\left|\overset{\rightarrow}{AB}\circ\left(\overset{\rightarrow}{ A C}\times\overset{\rightarrow}{ A S}\right)\right|=\frac{1}{6}\left| \det\left(\overset{\rightarrow}{ A B},\;\overset{\rightarrow}{ A C},\;\overset{\rightarrow}{ A S}\right)\right|$$
Hierbei sind \(\overrightarrow{AB}=\begin{pmatrix} -4\\-4\\-4 \end{pmatrix}\), \(\overrightarrow{AC}=\begin{pmatrix} -6\\-2\\4 \end{pmatrix}\) und \(\overrightarrow{AS}=\begin{pmatrix} -8\\8\\-6 \end{pmatrix}\)
Also:$$V=\frac{1}{6}\begin{vmatrix} -4 & -6 & -8 \\ -4 & -2 & 8\\ -4 & 4 & -6 \end{vmatrix}$$ Die Determinante kannst du mit der Regel von Sarrus (Jägerzaun) auflösen.