Extremwertaufgabe: Bsp. Maximale Größe der bedruckbaren Flächen in m²?

Question

Aufgabe:

Zu Werbezwecken soll ein rechteckiger Banner geschafft werden. Eine Werbeagentur bietet diesbezüglich einen Banner mit einem exakten Umfang von 10m an.

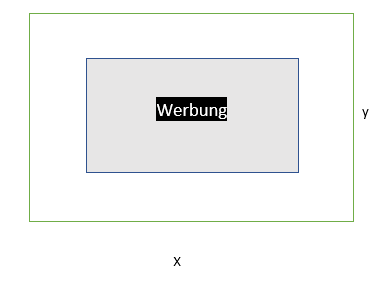
Allerdings sind die genauen Maße der Seitenlänge x und y noch festzulegen. Aus ästheschen Gründen und und zwecks besserer Lesbarkeit wird empfohlen, einen unbedruckten weißen Rand von jeweils 10cm oben und unten sowie 15cm rechts und links frei zu lassen.

Die bderuckbare Fläche (in Abbildung grau) des Werbebanners soll so groß wie möglich sein, um möglichst viele Werbefläche zu haben.

a) Zeigen Sie, dass sich die bderuckbare Fläche als Zielfunktion durch die Funktionsgleichung A(x) = -x²+4,9x-0,94 darstellen lässt!

b) Berechnen Sie die maximale Größe der bedruckbaren Flächen in m².

c) Ermitteln Sie nachvollziehbar die Seitenlängen x und y bei einer grötmöglichen Werbefläche in m.

d) Berechnen Sie den prozentualen Antiel der unbedruckten Fläche (weißer Rand) im Verhältnis zur Gesamtfläche des Banners.

Answer 1

Nebebnbedingung

2x + 2y = 10 --> y = 5 - x

Hauptbedingung

A = (x - 0.30) * (y - 0.20)

A = (x - 0.30) * (5 - x - 0.2)

A = (x - 0.30) * (4.8 - x)

A = - x^2 + 5.1·x - 1.44

Wenn ich x ersetze

A = (x - 0.30) * (y - 0.20)

A = (5 - y - 0.30) * (y - 0.20)

A = (4.7 - y) * (y - 0.20)

A = - y^2 + 4.9·y - 0.94

Hab ich einen Denkfehler gemacht oder der Aufgabensteller?

Comments

Was sind die Lösungen zu den jeweiligen Aufgaben?

---

Ich habe erstmal nur a) gemacht. Weil meine Lösung nicht mit der Vorgabe übereinstimmt.

a) Zeigen Sie, dass sich die bderuckbare Fläche als Zielfunktion durch die Funktionsgleichung A(x) = -x²+4,9x-0,94 darstellen lässt!

Ich erhalte den angegebenen Term wenn ich A(y) bilde und nicht wenn ich A(x) bilde.

Kontrolliere mal meine Lösung ob ich den Fehler gemacht habe oder der Lehrer, der die Aufgabe gestellt hat.

---

deins ist richtig die haben einen Fehler....

---

wie würden die anderen Aufgaben berechnet???

---

@Der_Mathecoach wie würdest du jetzt die anderen Aufgaben rechnen, ich denke deine Rechnung ist richtig.......

---

a) Zeigen Sie, dass sich die bedruckbare Fläche als Zielfunktion durch die Funktionsgleichung
A(x) = - x^2 + 4.9·x - 0.94 darstellen lässt!

A = (y - 0.3)·(x - 0.2)
A = (5 - x - 0.3)·(x - 0.2)
A = (4.7 - x)·(x - 0.2)
A = -x^2 + 4.9·x - 0.94

b) Berechnen Sie die maximale Größe der bedruckbaren Flächen in m².

A = -x^2 + 4.9·x - 0.94

Scheitelpunkt an der Stelle

Sx = -b/(2·a) = -4.9/(2·(-1)) = 2.45 m

Sy = A(2.45) = -2.45^2 + 4.9·2.45 - 0.94 = 5.0625 m^2

c) Ermitteln Sie nachvollziehbar die Seitenlängen x und y bei einer größtmöglichen Werbefläche in m.

Sx = (2.45 - 0.3) = 2.15 m

d) Berechnen Sie den prozentualen Anteil der unbedruckten Fläche (weißer Rand) im Verhältnis zur Gesamtfläche des Banners.

p = (x·y - A) / (x·y)
p = (2.45·2.15 - 5.0625) / (2.45·2.15) = 82/2107 = 0.0389 = 3.89%