Taylorreihenentwicklung für Funktionen mit 2 Variablen

Question

Hallo

in unserem Skript steht die Taylorreihenentwicklung für Funktionen mit 2 Variablen als irgendwie Summenzeichnen von paar Summen mit Mächtigkeiten die sich immer wechseln und was weiß ich

allerdings habe ich die Taylorentwicklung bis zu 2.ordnung auf einer Seite so umgeschrieben, was viel einfacher zum auswendig lernen ist :

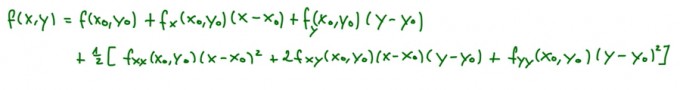
wisst Ihr wie die Umschreibung bis zur 3.Ordnung wäre ? weil ich komme mit den Summen nicht klar und brauche so eine Formel , wo ich die Werte einsetzen kann aber weiß nicht wie diese Formel für 3.Grades wäre.

Es wäre sehr nett wenn ihr schreibt , wie die für 3.Grades weitergeht entweder weil Ihr wisst wie die sein wird oder vielleicht habt Ihr sie in eurem Skript auch so umgeschrieben :)

Danke euch

Comments

Wenn Ihr auch so eine Formel für den Rest kennt , wäre es sehr nett die mal zu posten :) 

Answer 1

Hallo

$$\begin{aligned} T_{a,3}(x,y) &= f(a)+f_x(a)*(x-a_1)+f_y(a)*(y-a_2)\\ &+\frac{1}{2}f_{xx}(a)(x-a_1)^2 + f_{xy}(a)(x-a_1)(y-a_2)+\frac{1}{2}f_{yy}(a)(y-a_2)^2\\ &+\frac{1}{6}\left( f_{xxx}(a)(x-a_1)^3 + 3f_{xxy}(a)(x-a_1)^2(y-a_2) + 3f_{yyx}(a)(x-a_1)(y-a_2)^2+f_{yyy}(a)(y-a_2)^3\right)\\ =&f(a)+f_x(a)*(x-a_1)+f_y(a)*(y-a_2)\\ &+\frac{1}{2}f_{xx}(a)(x-a_1)^2 + f_{xy}(a)(x-a_1)(y-a_2)+\frac{1}{2}f_{yy}(a)(y-a_2)^2\\ &+\frac{1}{6} f_{xxx}(a)(x-a_1)^3 + \frac{1}{2}f_{xxy}(a)(x-a_1)^2(y-a_2) + \frac{1}{2}f_{xyy}(a)(x-a_1)(y-a_2)^2+\frac{1}{6}f_{yyy}(a)(y-a_2)^3\\ \end{aligned}$$

Gruß lul

Comments

Hi lul,

vielen vielen Dank ! könntest du auch so eine Formel für den Rest auch schreiben ? das wäre ja super und sehr nett von Dir

---

Hallo

 nein, dazu gibt es ja die Summenschreibweise, und an Hand der 4 ersten Glieder, solltest du die lesen lernen. Noch mehr aufzuschreiben ist unnütze und langwierige Arbeit. Du musst also das aufgeschriebene benutzen, dir selbst den Rest zu entschlüsseln, sooo schwer ist das nicht.

Gruß lul

---

:`(

okay Danke

---

Hey Lul ich hab gerade versucht mit der Summenschreibweise zu arbeiten. ich kriege die leider nicht hin :( bitte schreibe die Formel ich habe eine Klausur und es ist jetzt ein bisschen zu spät mich mit dieser Schreibweise zu beschäftigen

---

ich glaube ich hab's hingekriegt :) Dankeschön Lul !