L = 2·x + 4·√((50 - x)^2 + 50^2)
L = 4·√(x^2 - 100·x + 5000) + 2·x
L' = 2·(√(x^2 - 100·x + 5000) + 2·(x - 50))/√(x^2 - 100·x + 5000) = 0
√(x^2 - 100·x + 5000) + 2·(x - 50) = 0
√(x^2 - 100·x + 5000) = 100 - 2·x
x^2 - 100·x + 5000 = 4·x^2 - 400·x + 10000
3·x^2 - 300·x + 5000 = 0
x = 50 - 50·√3/3 = 21.13248654
L = 2·(50 - 50·√3/3) + 4·√((50 - (50 - 50·√3/3))^2 + 50^2) = 100·√3 + 100 = 273.2050807
Mein Streckennetz wäre 273.3 km lang, wenn ich mich da jetzt nicht verrechnet habe. Aufgabe des Fragestellers ist wie immer meine Rechnung sorgfältig zu prüfen, weil ich es nicht mache.
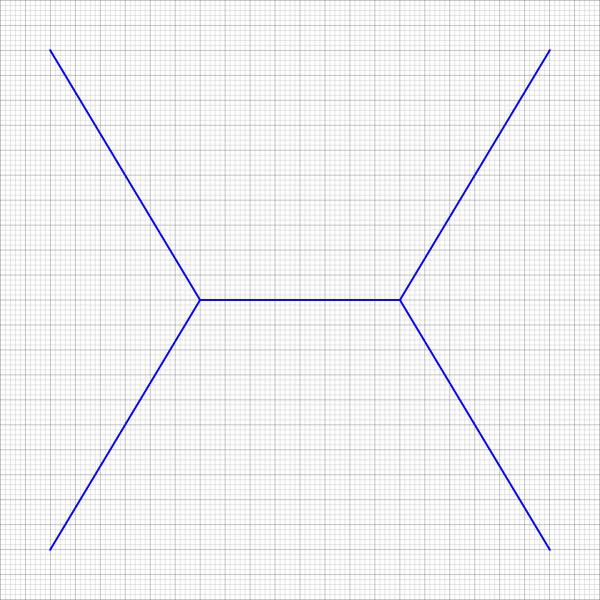
Eine Skizze meines Streckennetzes: