hallo
ich habe ein wenig recherchiert und ich denke mal, einfacher als über
die vektorrechnung wirst du es nicht hinbekommen.
ich habe es versucht so einfach und so verständlich wie möglich hinzubekommen,
guck mal:
__________________________________________________________________________
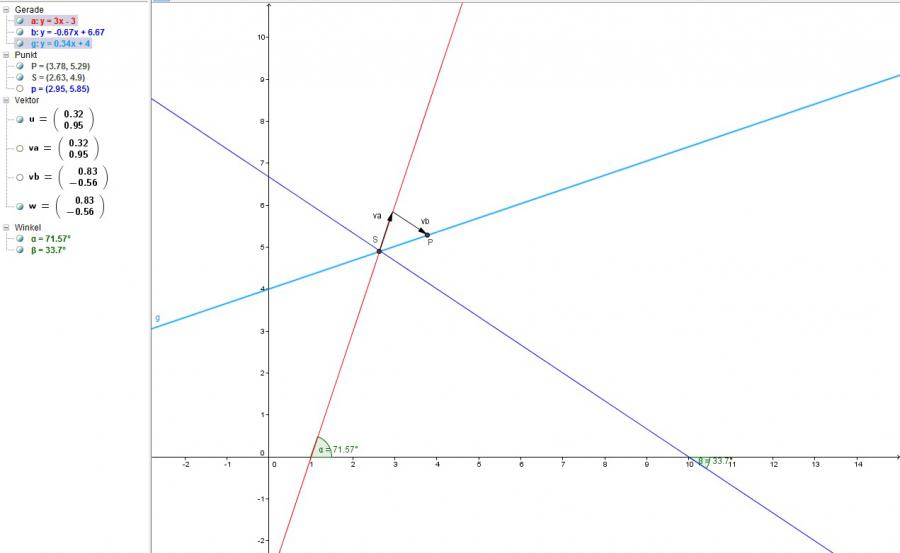
schnittpunktberechnung der geraden a = 3x-3 und b = -0.67x + 6.67
die x-koordinate des schnittpunktes bekommen wir, wenn wir
die beiden geradengleichungen gleichsetzen:
3x-3 = -0.67x + 6.67
x = 2.63
um y zu bekommen setzen wir x = 2.63 in eine der geradengleichungen ein
y = 3x-3
y = 3*2.63-3
y = 4.9
der schnittpunkt S der geraden a und b ist bei
x = 2.63 und y = 4.9
S (2.63, 4.9)
_____________________________________________________________________________
bestimmung des richtungvektors va, der in richtung der geraden a verläuft
wir kennen die steigung der geraden a, das ist m = 3.
damit kennen wir auch den winkel, den die gerade a mit der x-achse bildet:
α = arctan(3)
α = 71.57°
wir wählen für den richtungsvektor va den betrag 1 und erhalten:
für die x-komponente des vektors va: vax = cos α und
für die y-komponente des vektors va: vay = sin α
der richtungsvektor va in richtung der geraden a ist fertig:
va = (cos α, sin α)
va = (0.32, 0.95)
_____________________________________________________________________________
bestimmung des richtungvektors vb, der in richtung der geraden b verläuft
wir kennen die steigung der geraden b, das ist m = -0.67.
damit kennen wir auch den winkel, den die gerade b mit der x-achse bildet:
β = arctan(-0.67)
β = -33.7°
wir wählen für den richtungsvektor vb ebenfalls den betrag 1 und erhalten:
für die x-komponente des vektors vb: vbx = cos α und
für die y-komponente des vektors vb: vby = sin β
der richtungsvektor vb in richtung der geraden b ist fertig:
vb = (cos β, sin β)
vb = (0.83, -0.56)
_____________________________________________________________________________
jetzt addieren wir zum schnittpunt S die beiden richtungsvektoren va und vb
und erhalten den punkt P durch den die winkelhalbierende verläuft:
P = S + va + vb =
P = (2.63, 4.9) + (0.32, 0.95) + (0.83, -0.56)
P (3.78, 5.29)
wir sind fast am ziel. :-)
wir haben den schnittpunkt S der geraden a und b ermittelt, sowie
den punkt P. durch diese beiden punkte verläuft eine winkelhalbierende
(es gibt noch eine zweite :D).
wir ermitteln die steigung der winkelhalbierenden g:
m = Δy/Δx = (Py-Sy)/(Px-Sx) = (5.29-4.9)/(3.78-2.63) = 0.34
jetzt fehlt nur noch eine angabe, das ist der parameter b der
allgemeinen geradengleichung: y = mx + b
umstellen nach b:
b = y - mx
da wir wissen, durch welche punkte die winkelhalbierende verlaufen muss,
nämlich durch S und durch P, können wir für x und für y die koordinaten
von einem dieser punkte in die gleichung einsetzen, um b zu berechnen:
b = 4.9 - 0.34*2.63
b = 4
hier wie auch bei allen anderen werten haben wir gerundet.
und damit ist unsere geradengleichung für die winkelhalbierende fertig,
tadaaaa: g = 0.34x + 4
:-)