Gleichungen der beiden Winkelhalbierenden zwischen der x1-Achse und der x2-Achse?

Question

Aufgabe:

Geben sie für ein ebenes Koordinatensystem die Gleichungen der beiden Winkelhalbierenden zwischen der x1-Achse und der x2-Achse an.

Problem/Ansatz:

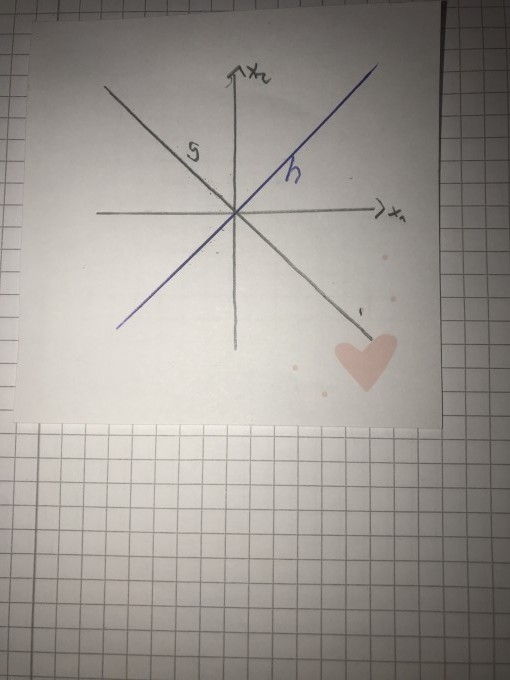
Habe mir eine kleine Skizze angefertigt (s. Anhang) und mir dann jeweils zwei Punkte auf der Gerade ausgesucht und dann die Gleichungen aufgestellt.

Habe jetzt für g: Vektor x= (0|0) + t* (1|1)

Und für h: Vektor x= (0|0) + t* (1|-1)

(Zahlen natürlich untereinander geschrieben weil es ja Vektoren sind)

Meine Frage jetzt, ist das so richtig, oder hab ich irgendwo einen Fehler gemacht?

Wäre sehr dankbar für eine kurze Rückmeldung.

Answer 1

Habe jetzt für g: Vektor x= (0|0) + t* (1|1)

Und für h: Vektor x= (0|0) + t* (1|-1)

(Zahlen natürlich untereinander geschrieben weil es ja Vektoren sind)

Das hast du richtig gemacht. Du hast Parametergleichungen aufgestellt. Es wäre noch möglich für beide Geraden eine Koordinatengleichung anzugeben.

Habe jetzt für g: Vektor (x1 | x2) = (0|0) + t* (1|1)

Und für h: Vektor (x1, x2) = (0|0) + t* (1|-1)

(Zahlen natürlich untereinander geschrieben weil es ja Vektoren sind)

Bei g ergibt sich x1 = t und x2=t. D.h x1 = t = x2 somit x2 = x1

oder wie du das vor früher kennst: y = x. (Steigung m = 1, y-Achsenabschnitt q = 0)

Bei h analog: Es ergibt sich x2 = -x1 oder (frühere Notation) y = -x (Steigung m = -1, y-Achsenabschnitt q = 0)