Sei abc ein (nicht gleichschenkliges) Dreieck.
Wie kann ich zeigen, dass die Schnittpunkte der äußeren Winkelhalbierenden mit den jeweils (erweiterten) gegenüberliegenden Seiten, alle auf einer Geraden liegen?
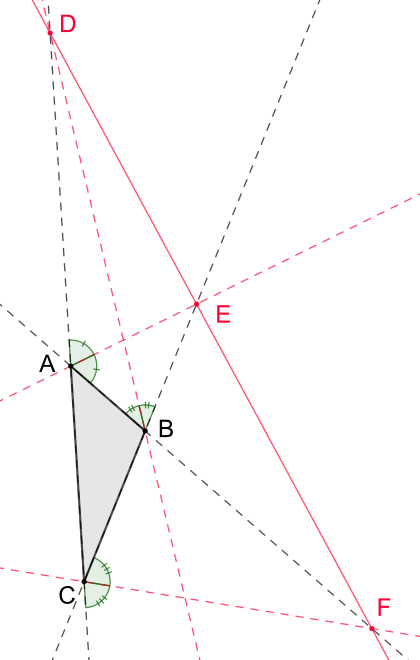
Ich versuche hier den Satz von Menelaus anzuwenden,
aber komme nicht weiter zu zeigen, dass TV(a;c,f)*TV(b;c,g)*TV(a;bc)=-1 gilt.
Angeblich soll die Lösung sehr kurz sein, ich weiß hier aber leider nicht weiter..
Danke für jegliche Hilfe & Zeit !